neal young / Young25Improved
-
working paper(2025)
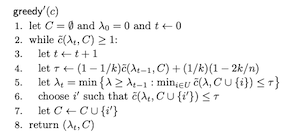 We give a polynomial-time approximation algorithm for the (not necessarily metric) \(k\)-Median problem.
The algorithm is an \(\alpha\)-size-approximation algorithm
for \(\alpha < 1+2\ln(n/k)\).
That is, it guarantees a solution having size at most \(\alpha\times k\),
and cost at most the cost of any size-\(k\) solution.
This is the first polynomial-time approximation algorithm to match
the well-known bounds of \(H_{\Delta}\) and \(1+\ln(n/\textsf{opt})\)
for unweighted Set Cover (a special case) within a constant factor.
It matches these bounds within a factor of 2.
The algorithm runs in time \(O(k\,m\log(n/k)\log m)\),
where \(n\) is the number of customers and \(m\)
is the instance size.
We give a polynomial-time approximation algorithm for the (not necessarily metric) \(k\)-Median problem.
The algorithm is an \(\alpha\)-size-approximation algorithm
for \(\alpha < 1+2\ln(n/k)\).
That is, it guarantees a solution having size at most \(\alpha\times k\),
and cost at most the cost of any size-\(k\) solution.
This is the first polynomial-time approximation algorithm to match
the well-known bounds of \(H_{\Delta}\) and \(1+\ln(n/\textsf{opt})\)
for unweighted Set Cover (a special case) within a constant factor.
It matches these bounds within a factor of 2.
The algorithm runs in time \(O(k\,m\log(n/k)\log m)\),
where \(n\) is the number of customers and \(m\)
is the instance size.
© Copyrights are reserved by the publishers.
Download for personal and limited academic use only.