neal young / Khuller96Strongly
-
Discrete Applied Mathematics 69(3):281-289(1996)
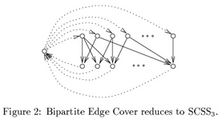The MEG (minimum equivalent graph) problem is, given a
directed graph, to find a small subset of the edges that
maintains all reachability relations between nodes. The
problem is NP-hard; This paper gives a proof that, for graphs
where each directed cycle has at most three edges, the MEG
problem is equivalent to maximum bipartite matching, and
therefore solvable in polynomial time. This leads to an
improvement in the performance guarantee of the previously
best approximation algorithm for the general problem, from
``Approximating the minimum equivalent digraph'' [1995].
(This result was improved by Berman et al, WADS, 2009.)
© Copyrights are reserved by the publishers.
Download for personal and limited academic use only.