neal young / Fekete97Network
-
Journal of Algorithms 24(2):310-324(1997)
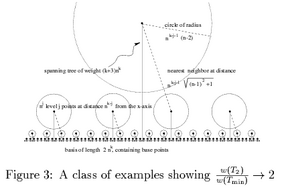 The problem considered is the following. Given a graph with
edge weights satisfying the triangle inequality, and a degree
bound for each vertex, compute a low-weight spanning tree such
that the degree of each vertex is at most its specified
bound. The problem is NP-hard (it generalizes Traveling
Salesman (TSP)). The paper describes a network-flow heuristic
for modifying a given tree T to meet the constraints. Choosing
T to be a minimum spanning tree (MST) yields approximation
algorithms with performance guarantee less than 2 for the
problem on geometric graphs with Lp-norms. The
paper also describes a Euclidean graph whose minimum TSP costs
twice the MST, disproving a conjecture made in [Low-degree
spanning trees of small weight].
The problem considered is the following. Given a graph with
edge weights satisfying the triangle inequality, and a degree
bound for each vertex, compute a low-weight spanning tree such
that the degree of each vertex is at most its specified
bound. The problem is NP-hard (it generalizes Traveling
Salesman (TSP)). The paper describes a network-flow heuristic
for modifying a given tree T to meet the constraints. Choosing
T to be a minimum spanning tree (MST) yields approximation
algorithms with performance guarantee less than 2 for the
problem on geometric graphs with Lp-norms. The
paper also describes a Euclidean graph whose minimum TSP costs
twice the MST, disproving a conjecture made in [Low-degree
spanning trees of small weight].
© Copyrights are reserved by the publishers.
Download for personal and limited academic use only.