• Journal of Scheduling 18(6):545-560(2015); (ICALP '13);

  With Marcin Bienkowski, Jaroslaw Byrka, Marek Chrobak, Neil Dobbs, Thomas Nowicki, Maxim Sviridenko and Grzegorz Swirszcz
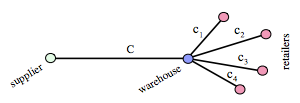  The Joint Replenishment Problem (JRP) is a fundamental optimization problem in supply-chain management, concerned with optimizing the flow of goods over time from a supplier to retailers. Over time, in response to demands at the retailers, the supplier sends shipments, via a warehouse, to the retailers. The objective is to schedule shipments to minimize the sum of shipping costs and retailers' waiting costs. We study the approximability of JRP with deadlines, where instead of waiting costs the retailers impose strict deadlines. We study the integrality gap of the standard linear-program (LP) relaxation, giving a lower bound of 1.207, and an upper bound and approximation ratio of 1.574. The best previous upper bound and approximation ratio was 1.667; no lower bound was previously published. For the special case when all demand periods are of equal length we give an upper bound of 1.5, a lower bound of 1.2, and show APX-hardness.

  Journal version of [2013].

  • more...
  •   full text
    
  •   bibtex
    
  •   google scholar
    
  •   doi
    

© Copyrights are reserved by the publishers.
Download for personal and limited academic use only.