Design and Analysis of Algorithms Neal Young

Computer Science 45

Notes on generating functions My intention here is to just give you a brief introduction to pique your interest and familiarize you with the ideas. Check out the reference by Vitter and Flajolet [3] for further and more comprehensive info on generating functions. Another reference for discrete math in general is the text Concrete Math [2]. I expect you could find Mathematica or Maple packages to play with on the net, one possible lead is [1].

Example - the symbolic method.

How many distinct n-node binary trees are there? The ordinary generating function for the set of binary trees is

where is the number of binary trees of size n. In the function b, there is one term of ``size'' n for each tree of size n. Postponing for a minute the question of what purpose this serves, can we find a simpler form for the function b? Here is a simple set of rules defining the binary trees:

1. The tree consisting of a single node is a binary tree.
2. If a tree T is a binary tree, then the tree formed by creating a new root r and making T the single subtree of r is a binary tree.
3. If trees and are binary trees, then the tree formed by creating a new root r and making and the left and right subtrees of r is a binary tree.

From this set of rules we can see the following equivalence:

Here `` '' represents a single node and `` '' means there is a size-preserving bijection (a one-to-one and onto function f such that the size of x equals the size of f(x)) between the set on the left and the set on the right. Replacing each root `` '' by a ``z'' (a term of ``size'' 1) and replacing the set union by addition yields the corresponding equivalence:

Solving for b(z) using the quadratic formula yields

From this closed form and a little algebra, we can see that b(z) is well-defined as long as -- for larger values, the term inside the square root becomes negative. Amazingly, from this it follows directly (for reasons discussed below) that grows roughly like . With a little more work, an exact form for can be obtained.

Example - recurrence relations.

The Fibonacci numbers are defined by the following recurrence:

The corresponding generating function is Can we find a simple form for f(z)? Using the recurrence, we get

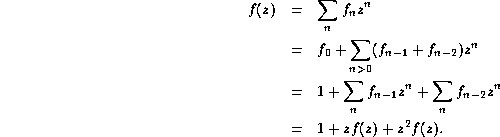
Solving for f yields

From this we can see that f is well-defined as long as z is less than -- the smallest root of . From the general principle described below, it follows that grows roughly like .

Estimating the rate of growth from the smallest singularity.

In the above examples, we used the following rule of thumb:

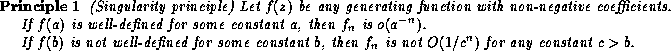
We can summarize this by saying that the best exponential approximation to the rate of growth of is , where r is the smallest singularity of f(z), in other words, r is the largest value such that for all z<r, f(z) is well-defined.

Why is this the case? If f(a) is well-defined, then the infinite sum converges. Its terms must tend to zero as n tends to infinity:

This establishes the first part of the principle: .

On the other hand, let b and c be as in the second part of the principle: f(b) is not well-defined and b<c. Suppose for contradiction that is . Then , so that

This contradicts our assumption that f(b) was not well-defined.

Symbolic derivations - general principles.

Here are a few general principles for deriving generating functions: Suppose sets A and B have generating functions a(z) and b(z), respectively.

• has generating function a(z)+b(z), provided A and B are disjoint.
• (the Cartesian product) has generating function a(z)b(z).
• (the Cartesian product of A with itself k times) has generating function .
• has generating function . ( is called the Kleene closure of A, its elements are the finite sequences of elements from A)

(The rule for Cartesian products assumes that the ``size'' of an element is the sum of the sizes of and . This was the case in the binary tree example. The subsequent rules have a similar assumption.)

Why are these principles true? Take the Cartesian product rule for example. For every element and , there is a term in a(z) and a term in b(z), where i and j are the sizes of and , respectively. In the product a(z)b(z), the pair thus contributes a single term of ``size'' equal to the size of the pair . More formally, we can write

Since the number of pairs of size n in is , this proves the principle.

A canonical example.

How many k-digit decimal numbers are there whose digits sum to n? Let D be the set of digits . For this problem, we think of each digit as having a size equal to itself. With this interpretation, the generating function for d(z) is .

The set of k-digit numbers is then . The generating function for is . Here the ``size'' we associate with a k-digit number is just the sum of the sizes of the digits.

The singularity principle says that the nth coefficient grows like -- this time it's not so useful! On the other hand, note that for fixed k, this generating function has only finitely many terms, so we have to be a little more careful when asking questions about the asymptotics.

Arbitrary-degree rooted trees.

Let be the number of distinct rooted trees of size n. We can define the set of rooted trees as follows:

1. A single node is a rooted tree.
2. If is any finite sequence of rooted trees, then a new rooted tree can be formed by creating a new root node r and making the roots of the trees in the sequence the children of r.

In fact, the first rule is the special case of the second that occurs when k=0, so we can omit it. This gives the equivalence for the set T of rooted trees:

(Recall that represents finite sequences of elements of T.) The generating function t(z) thus satisfies

Solving for t(z) using the quadratic formula yields

From the singularity principle, it follows that grows roughly like .

Exact answers.

The singularity principle is useful for getting rough estimates of the exponential rate of growth of the coefficients of a generating function. Even more can be said about a generating function from its singularities, however, the proper tool for this is complex analysis and we don't pursue it further here.

Instead we give a few simple examples where exact expressions can be obtained for the coefficients.

A few standard series.

• . This is the generating function for any set where there is exactly one item of each size.
• . This function is an example of an exponential generating function, which we don't go into here. These kinds of generating functions are useful for counting ``labelled'' structures -- for instance, binary trees where each node is assigned a number; another example is counting restricted classes of functions or permutations.
• . This is the generating function for the binomial coefficients. When m is an integer, the nth coefficient represents the number of size-n subsets of a set of size m.

Differentiation.

Suppose you have a simple form f(z) for the generating function , and you want a simple form for -- that is, you want to introduce a linear term. Note that , so that the answer you want is just zf'(z). For instance, applying this to the generating function gives .

You can also use differentation to get the exact form for the coefficients. The general rule is

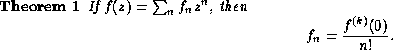
Here represents the kth derivative of f. To prove it, first use induction to show that , then substitute k=n and z=0 (so all terms but the leading one drop out) to get .

Repeated differentation can often be messy, but not always. For example,

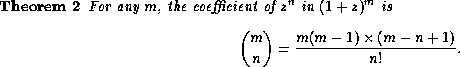
This holds for arbitrary m, not just integer values. To prove it, just note that differentiating n times yields and then apply the preceding theorem.

Substitution.

From it follows by substituting 2z for z that . Similarly by substituting for z one obtains .

Partial fractions.

Recall that the generating function for the Fibonacci numbers is

Factor the denominator and separate into partial fractions:

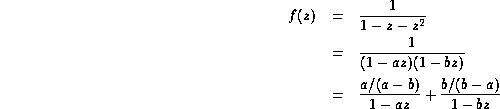
Here 1/a and 1/b are the roots of : . Letting denote the coefficient of in f(z), we have

References

1

J. S. Devitt. Combinatorial objects and their generating functions: A Maple class room environment. In Thomas Lee, editor, Mathematical Computation with Maple V: Ideas and Applications: Proceedings of the Maple Summer Workshop and Symposium, University of Michigan, Ann Arbor, June 28-30, 1993, pages 20-26, Boston, MA, USA, 1993. Birkhäuser.

2

Ronald L. Graham, Donald E. Knuth, and Oren Patashnik. Concrete Mathematics. Addison-Wesley, Reading, MA, USA, second edition, 1994.

3

Jeffrey Scott Vitter and Philippe Flajolet. Average-Case Analysis of Algorithms and Data Structures, chapter 9. Elsevier Science Publishers B.V., 1990. ISBN 0-444-88075-5.

About this document ...

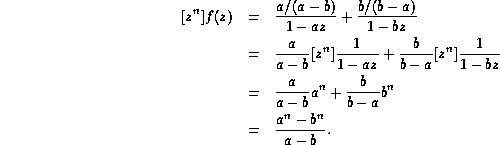
This document was generated using the LaTeX2HTML translator Version 96.1 (Feb 5, 1996) Copyright © 1993, 1994, 1995, 1996, Nikos Drakos, Computer Based Learning Unit, University of Leeds.

The command line arguments were:
latex2html -no_navigation -split 0 gen-fns.

The translation was initiated by Neal Young on Fri Apr 18 09:47:38 EDT 1997

...here.

Some refinement is possible even without complex analysis. Here's a hint about pinning down the polynomial term.

Suppose that f(r) is well-defined but f(z) is not well-defined for z>r. Compare the sum (which converges) to the sum (which diverges). This will give you better upper bounds on . Suppose further that f' (the derivative of f) is not well-defined at r. Compare the sum (the derivative at r, which diverges) to (which converges). This will give you better lower bounds.

If you are not so lucky that f(r) is well-defined and f'(r) isn't, then consider integrating or differentiating f several times so that the resulting function has the property you want. Recall that each differentation introduces a linear term in each coefficient, whereas integration factors one out.