neal young / Young94Bound
-
Technical Report, School of ORIE, Cornell University 1103(1994)
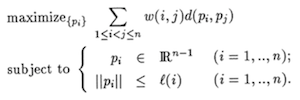We consider the problem of choosing Euclidean points
to maximize the sum of their weighted pairwise distances,
when each point is constrained to a ball centered at the origin.
We derive a dual minimization problem and show strong duality holds
(i.e., the resulting upper bound is tight)
when some locally optimal configuration of points is affinely independent.
We sketch a polynomial time algorithm
for finding a near-optimal set of points.
© Copyrights are reserved by the publishers.
Download for personal and limited academic use only.