neal young / Lipton94Simple
-
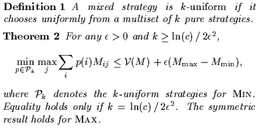Von Neumann's Min-Max Theorem guarantees that each player of a
zero-sum matrix game has an optimal mixed strategy. This paper
gives an elementary proof that each player has a near-optimal
mixed strategy
that chooses uniformly at random from a multi-set of pure
strategies of size logarithmic in the number of pure
strategies available to the opponent.
For exponentially large games, for which even representing an optimal mixed strategy can require exponential space, it follows that there are near-optimal, linear-size strategies. These strategies are easy to play and serve as small witnesses to the approximate value of the game.
As a corollary, it follows that every language has small ``hard'' multi-sets of inputs certifying that small circuits can't decide the language. For example, if SAT does not have polynomial-size circuits, then, for each \(n\) and \(c\), there is a set of \(n^{O(c)}\) Boolean formulae of size \(n\) such that no circuit of size \(n^c\) (or algorithm running in time \(n^c\)) classifies more than two-thirds of the formulae successfully.
The "simple strategies" observation was generalized to Nash equilibrium by Lipton et al. in their paper Playing large games using simple strategies.
© Copyrights are reserved by the publishers.
Download for personal and limited academic use only.