neal young / Khuller95Balancing
-
Algorithmica 14(4):305-322(1995); SODA'93
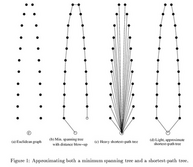 This paper has a simple linear-time algorithm to find a
spanning tree that simultaneously approximates a shortest-path
tree and a minimum spanning tree. The algorithm provides a
continuous trade-off: given the two trees and \(\epsilon > 0\), the
algorithm returns a spanning tree in which the distance
between any vertex and the root of the shortest-path tree is
at most \(1+\epsilon\) times the shortest-path distance, and yet
the total weight of the tree is at most \(1+2/\epsilon\) times the
weight of a minimum spanning tree. This is the best trade-off
possible.Journal version of [1993].
This paper has a simple linear-time algorithm to find a
spanning tree that simultaneously approximates a shortest-path
tree and a minimum spanning tree. The algorithm provides a
continuous trade-off: given the two trees and \(\epsilon > 0\), the
algorithm returns a spanning tree in which the distance
between any vertex and the root of the shortest-path tree is
at most \(1+\epsilon\) times the shortest-path distance, and yet
the total weight of the tree is at most \(1+2/\epsilon\) times the
weight of a minimum spanning tree. This is the best trade-off
possible.Journal version of [1993].
© Copyrights are reserved by the publishers.
Download for personal and limited academic use only.