neal young / Hakimi97Orienting
-
Information Processing Letters 63(5):229-235(1997)
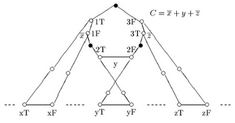The paper focuses on two problems: (i) how to orient the edges
of an undirected graph in order to maximize the number of
ordered vertex pairs \((x,y)\) such that there is a directed path
from \(x\) to \(y\), and (ii) how to orient the edges so as to
minimize the number of such pairs. The paper describes
a quadratic-time algorithm for the first problem, and a proof
that the second problem is NP-hard to approximate within some
constant \(1+\epsilon > 1\). The latter proof also shows that the
second problem is equivalent to ``comparability graph
completion''; neither problem was previously known to be
NP-hard.
© Copyrights are reserved by the publishers.
Download for personal and limited academic use only.