neal young / Gelal09Topology
-
IEEE Transactions on Mobile Computing 8(5):590-605(2009); SECON'06
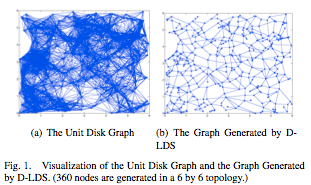With fully directional communications, nodes must track and periodically update the positions of their discovered neighbors, so that communication with these neighbors is feasible when needed. If tracking fails, neighbors that move out of the directional footprint will need to be rediscovered. The tracking process introduces an overhead, which increases with the number of discovered neighbors. The overhead can be reduced if each node maintains only a subset of its neighbors; however, this may increase the hop count of paths between nodes, i.e., causes a hop stretch. In this work, we study the tradeoffs between node degree and hop stretch. We first design a topology control algorithm to optimize this tradeoff. For the purposes of this design, we assume that nodes perform circular directional transmissions to communicate with the nodes in their directional range; in this way, the network can be modeled as a unit disk graph (UDG). Given a UDG G, our algorithm finds a sparse subgraph G' with a maximum node degree of 6, and connecting each node pair u, v by a path of length
hopsG'(u,v) = O(hopsG(u,v) + log \delta),
where \delta is the maximum degree in G, and hopsG(u,v) denotes the length of the shortest path between u and v in graph G. We show that this result is near optimal. Based on the insights gained from the above design, we next construct a more practical scheme, which integrates topology control with fully directional neighbor discovery and maintenance. The simulated performance of our practical scheme is only slightly worse than the theoretical optimal performance in terms of node degree and path stretch.Journal version of [2006].
© Copyrights are reserved by the publishers.
Download for personal and limited academic use only.