neal young / Cohen18Balanced
-
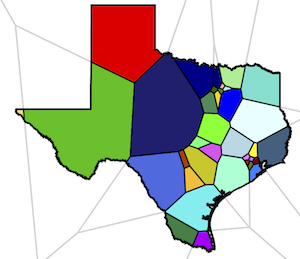We consider the problem of political redistricting: given the locations of people in a geographical area (e.g. a US state), the goal is to decompose the area into subareas, called districts, so that the populations of the districts are as close as possible and the districts are "compact" and "contiguous," to use the terms referred to in most US state constitutions and/or US Supreme Court rulings.
We study a method that outputs a solution in which each district is the intersection of a convex polygon with the geographical area. The average number of sides per polygon is less than six. The polygons tend to be quite compact. Every two districts differ in population by at most one (so we call the solution balanced).
In fact, the solution is a centroidal power diagram: each polygon has an associated center in R3 such that
- the projection of the center onto the plane z = 0 is the centroid of the locations of people assigned to the polygon, and
- for each person assigned to that polygon, the polygon center is closest among all centers. The polygons are convex because they are the intersections of 3D Voronoi cells with the plane.
The solution is, in a well-defined sense, a locally optimal solution to the problem of choosing centers in the plane and choosing an assignment of people to those 2-d centers so as to minimize the sum of squared distances subject to the assignment being balanced.
A practical problem with this approach is that, in real-world redistricting, exact locations of people are unknown. Instead, the input consists of polygons (census blocks) and associated populations. A real redistricting must not split census blocks. We therefore propose a second phase that perturbs the solution slightly so it does not split census blocks. In our experiments, the second phase achieves this while preserving perfect population balance. The district polygons are no longer convex at the fine scale because their boundaries must follow the boundaries of census blocks, but at a coarse scale they preserve the shape of the original polygons.
© Copyrights are reserved by the publishers.
Download for personal and limited academic use only.