neal young / Chrobak15Optimal
-
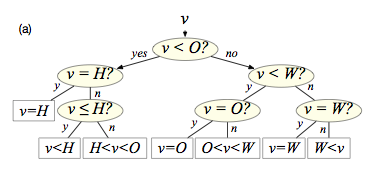In 1971, Knuth gave an \(O(n^2)\)-time algorithm for the classic problem of finding an optimal binary search tree. Knuth's algorithm works only for search trees based on 3-way comparisons, while most modern computers support only 2-way comparisons (e.g., \(<\), \(\le\), \(=\), \(\ge\), and \(>\)). Until this paper, the problem of finding an optimal search tree using 2-way comparisons remained open --- poly-time algorithms were known only for restricted variants. We solve the general case, giving (i) an \(O(n^4)\)-time algorithm and (ii) an \(O(n\log n)\)-time additive-3 approximation algorithm.
For finding optimal binary split trees, we (iii) obtain a linear speedup and (iv) prove some previous work incorrect.
© Copyrights are reserved by the publishers.
Download for personal and limited academic use only.