|
|
|
|
 |
|
* CormenEtal? problem 23-2 (Articulation points) |
|
* CormenEtal? problem 23-2 (Articulation points) |
A cut vertex (in a connected, undirected graph) is a vertex whose removal disconnects the graph.
A simple algorithm for identifyiing cut vertices:
1. For each vertex w, remove w from the graph and see if the graph becomes disconnected, using DFS or BFS.
Time for this one is O(n(n+m)), where n=#vertices, m=#edges.
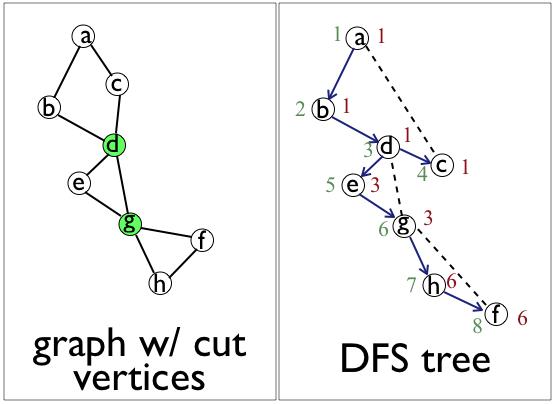
To get a faster algorithm, consider the DFS tree of the graph. In particular, consider the back edges:
The graph is on the left, the cut vertices are in green.
The DFS tree is on the right, the back edges are the dotted edges.
Claim: A non-root vertex U is a cut vertex if and only if one of its children W in the DFS tree has the following property:
To determine whether this property holds for a vertex, define:
Claim: A non-root vertex U in the DFS tree is a cut vertex if and only if one of its children W in the DFS tree has:
(Prove this later.)
Claim: A root vertex is a cut vertex if and only if it has two or more children in the DFS tree (using just tree edges).
(Prove this later.)
Claim: the low[] numbers satisfy the following recurrence relation:
(Prove this later.)
To finish, the low[] numbers can be computed bottom-up using the DFS tree using the recurrence. This computation takes O(n+m) time.
To summarize, here is the outline of an O(n+m)-time algorithm for identifying cut vertices:
1. A non-root vertex U is a cut vertex if and only if one of its children W in the DFS tree has the following property:
2. The root vertex of the dfs tree is a cut vertex if and only if it has two or more children in the DFS tree (using just tree edges).
3. The low numbers satisfy the following recurrence relation:
To verify the algorithm, we need to consider carefully whether the claims are true. In particular, are we convinced the claims will hold when the algorithms are run on any input.
Next we will do this, partly, to give an idea of what's involved.
For the first claim to be true, it must be that, for any input,
and
The second part (1B) is easy to argue for. If U has a child W, with no descendant of W having a back edge going to a vertex above U, then removing W disconnects the child from the parent of W.
The first part (1A) is a little less obvious. We tried to come up with a line-by-line justification:
This seems to be a convincing and general argument that (1A) is true. If we accept this argument, then we believe (1A) is true. If we accept that (1B) is also true, then we believe claim (1).
Note that to really convince ourselves that the algorithm is correct, we need to verify also that claims (2) and (3) are correct. We leave these as exercises (for claim (3), see DynamicProgramming).