Counting paths from a vertex S to a vertex T in a DAG (directed acyclic graph)
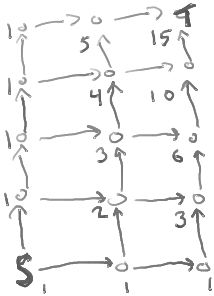
How many distinct paths are there from S to T in this graph?
Each vertex is labeled with the number of paths from S to that vertex.
Note that each label is the sum of the labels of the vertices coming into that vertex. (Except at S, which has label 1.)
In fact, this is true in general in any acyclic digraph:
Define N(V) = the number of distinct paths from S to V.
Then N() satisfies the following recurrence relation:
- N(S) = 1 and
- N(V) = ∑W : (W,U) ∈ E N(W).
This recurrence relation leads to a linear-time algorithm for counting the number of S->T paths in a given DAG.
Namely,
1. Topologically sort the vertices. 2. Set N[S] = 1, and, for each vertex V before S in the ordering, set N[V] = 0. 3. For each vertex V after S in the ordering, in order of the ordering, do: 4. Set N(V) = ∑W:(W,U)∈ E N(W). 5. Return N(T)
In order to verify that the algorithm is correct, we have to convince ourselves that the recurrence relation is true.
How do we do that?
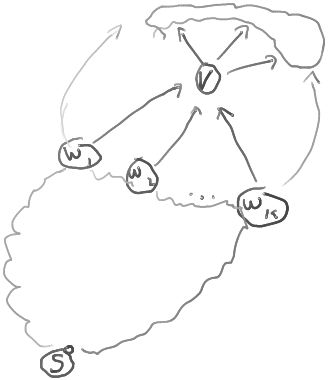
We want to show that the number of distinct paths from S to V in the above diagram equals the number of distinct paths from S to any W1,W2,...,Wk.
This may seem obvious, but let's do a careful proof.
Let P be the set of paths from S to any Wi.
Form a set P' of paths as follows:
- For each path p in P, add the vertex V to the end of the path to get a longer path p'
- The set of paths P' consists of the paths p' obtained in this way.
Note that the size of P' is the same as the size of P, because for each path p in P there is exactly one path p' in P'. (All the paths p' produced by the process are distinct because all the paths in P are distinct, and adding a vertex to each of two distinct paths yields two distinct paths.)
I claim that P' is exactly the set of paths from S to V.
Clearly every path in P' is a path from S to V, since each Wi has an edge to V.
Conversely, every path from S to V is in P', because every path from S to V is of the form p' = (p,v) where p is a path from S to some Wi. (In words, every path from S to V goes through some Wi just before reaching V.
In sum, we know:
- P is the set of paths from S to any Wi
- P' is the set of paths from S to V
- P and P' are the same size.
Thus, the recurrence is correct.
To test yourself, figure out what happens in a digraph that contains cycles. Is the recurrence still true? Answer this question assuming we want to count paths with cycles, where we consider two paths to be different if they don't use exactly the same set of edges (they may re-use an edge a different number of times). Then answer it assuming we want to count only paths without cycles.