Transitive Closure
(Read section 6.4.2 of the text.)
Given a digraph G = (V,E), we want to compute a matrix M such that M[i,j] is true if there is a path from i to j.
One way is to iterate over all vertices and do a depth-first or breadth-first search starting from each vertex to see what vertices are reachable from it. This takes O(n(n+m)) time.
Here's another more complicated way.
Order the vertices v1,v2,...,vn in some arbitrary way.
Define M[i,j,k] to be true if there is a path from i to j that goes through only the first k vertices v1,...,vk. (That is, i and j need not be in the set of k vertices, but all the other vertices on the path must be.)
For example:
M[i,j,0] = true if there is an edge from i to j in E.
M[i,j,1] = true if there is an edge from i to j or edges (i,1) and (1,j)
M[i,j,n] = true if there is any path from i to j.
Claim: M[i,j,k] = true iff (M[i,j,k-1] = true or (M[i,k,k-1] = true and M[k,j,k-1] = true) )
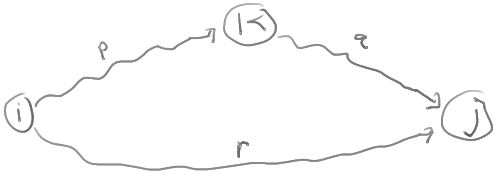
To see this, consider the diagram:
Any path from i to j going only through vertices in the set {1,2,...,k} is of one of the following two forms:
- The path goes from i to j using only vertices in the set {1,2,...,k-1}.
- The path goes from i to k using only vertices in the set {1,2,...,k-1} and then goes from k to j using only vertices in th set {1,2,...,k-1}.
This recurrence leads to the following algorithm:
1. Initialize M[i,j] = false for all i,j. 2. Set M[i,j] = true for each edge (i,j) in E. 3. For k = 1,2,...,n 4. For i = 1,2,...,n 5. For j = 1,2,...,n 6. M[i,j] = M[i,j] || (M[i,k,k-1] && M[k,j,k-1]) 7. Return M.
The algorithm runs in n3 time.
This isn't particularly fast, however we will see later (ShortestPathsByDP) how to modify the algorithm to compute shortest paths (a slightly more difficult problem).
References
- DynamicProgramming
- GoodrichAndTomassia section 6.4.2 - Transitive Closure