Consider the following sequence of Q=64 bits. Every R=7th bit (starting with the 3rd) is 1, the others (represented by '.') are 0:
From this sequence, form the corresponding 0-1 vector, and apply the discrete Fourier transform. That is, multiply the vector by the Q by Q matrix whose (A,C) entry is the complex number exp(2*Pi*I*(A-1)*(C-1)/Q)/sqrt(Q).
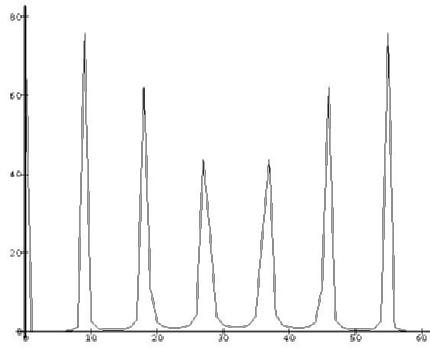
The resulting vector V of Q complex numbers will be roughly periodic, in the sense that only those entries whose indices are close to a multiple of Q/R will have large magnitude. You can see this in the following plot. The X-axis represents the index X, while the Y-axis represents the squared magnitude of the complex number V[X] (for X=1..N). Note that if R divides Q exactly, then the "off-period" entries will be zero and the spikes will all be the same height. In general, the heights of the spikes will vary by at most a small constant factor.

The following maple script produced the plot:
> with(linalg):
------------------------------------------------------------------------------
> n := 64: r := 7:
------------------------------------------------------------------------------
> F := matrix(n, n, (a,c) -> E^(2*Pi*I*(a-1)*(c-1)/n)):
-------------------------------------------------------------------------------
> V := vector(n, a-> if (a mod r = 3) then 1 else 0 fi):
-------------------------------------------------------------------------------
> evalm(V);
[ 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0,
0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0,
1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0 ]
-------------------------------------------------------------------------------
> T := evalf(evalm(F*V)):
-------------------------------------------------------------------------------
> S := [[c,abs(T[c+1])^2] $c=0..n-1]:
-------------------------------------------------------------------------------
> plot("):
-------------------------------------------------------------------------------
> evalf(n/r);
9.142857143
-------------------------------------------------------------------------------