Interface Exploration for Reduced Power in Core-Based Systems

Tony Givargis, Frank Vahid
Department of Computer Science and Engineering
University of California
Riverside, CA 92521
{givargis, vahid}@cs.ucr.edu
http://www.cs.ucr.edu/~dalton

Abstract

Reducing power dissipation is becoming more important in the design of embedded systems. Core-based system design opens up the opportunity for exploring different bus interfaces in order to optimize for reduced power. We give a first approach for exploring a range of possible bus configurations, such as width and coding schemes, for a given set of communication channels. Our approach uses power estimation formulas, for fast performance. We use this approach to explore different bus interfaces for a real GPS navigation system in order to select the optimal bus interface for minimum power consumption.

1. Introduction

In recent years, embedded system designers have been faced with the need to reduce power consumption. A system's power can be broken into two components. The first component is internal circuit capacitance times the average internal circuit transitions, while the second component is external bus capacitance times the average external bus transitions. The distribution of power among these two components is anywhere between 10% bus I/O [11] to 80% bus I/O [12], depending on the nature of application, implementation technology, etc. On the average, the I/O and system busses in a typical IC consume half of the total chip power [7, 13]. Much has been done in reducing the internal circuit power, but buses, often considered highly rigid and unalterable, have not been greatly optimized for power. Recent trends in technology have made it possible to explore buses for reduced power.

In the past, most IC components had a fixed number of I/O pins and required a pre-determined communication protocol. Today, increase in chip capacities has made it possible to integrate an entire system on a single chip in what is known as system-on-chip design. To increase efficiency, designers interconnect pre-designed cores, description of components, to implement a system. Cores are flexible and their interfaces can often be parameterized. This flexibility makes it possible to consider different bus sizes, partitions and encoding schemes for interconnecting components.

As an added incentive for designing buses for reduced power, with sub- micron technology, wires will consume most of a system's power when compared to transistors [9], hence reducing wires at the cost of increasing transistors will reduce overall power consumption.

In this paper, we give an approach for exploring different bus interfaces for reduced power. In section 2, we give a summary of related work. In section 3, we define the bus model that we focus on in the rest of the paper. In section 4,we give an algorithm for exploring different bus interfaces. In section 5, we define power cost functions or approximation formulas. In section 6, we apply our algorithm on a real GPS navigation system. In the remainder of the paper, we state future work and give our conclusion.

2. Previous Work

Much work has been done in modeling and estimating power in IC design at a high-level [3, 8]. These modeling and estimation techniques assume one average circuit capacitance for both internal and external power computations. We separate these two components, in our estimations, to account for buses with much larger capacitance compared to the internal circuits. Other work has looked at partitioning a circuit on the functional level in order to reduce total communication among various components [14]. Functional partitioning will reduce total power, including bus power. Once the partitioning is performed, exploring different bus widths and encoding schemes can further reduce bus power.

One such encoding scheme is bus-invert. Bus-invert coding has been a significant contribution in reducing bus power [9]. This method uses an extra control line and extra circuit logic to compute the Hamming distance (bit transitions) between to consecutive data items. If the Hamming distance is greater than ½ the bus width, then the control line is asserted and the inverted data is send over the bus. According to [9], bus-invert can save up to 25% of total bus transitions.

By using more than one extra control line, as used in bus-invert, a generalized scheme, called limited-weight codes [1, 2], can be used to encode data items for reduced average transitions. For instance, imagine a 4-bit channel transmitting on a 16-bit bus, where each data value corresponds to one of the 16 lines being asserted. Here, only 2 transitions are required to send a new data item. One for deactivating the old asserted signal for the old data item, and one for activating a new signal for the new data time.

In [4, 5, 6], techniques have been developed to automate interfacing of components. These techniques explore bus sizes and partitions among buses with the goal of trading off size and performance. We focus on optimizing for power only. These techniques can be combined with our work, to generate optimal bus, performance, power, and size.

3. Problem Formulation

We begin by defining the bus model used throughout this paper. A communication channel is an abstract link used by one device to send/receive data to/from another device. We denote an item to be a single data value sent or received over a communication channel. We associated with each communication channel a data-size, number of bits in an item, and a transfer-rate, number of items sent/received per second. We distinguish a set of homogeneous communication channels all having equal data size from a set of heterogeneous communication channels with mixed data sizes. All communication channels share a single bus. This model is commonly used in micro-controllers having a processor surrounded by a number of peripheral devices. 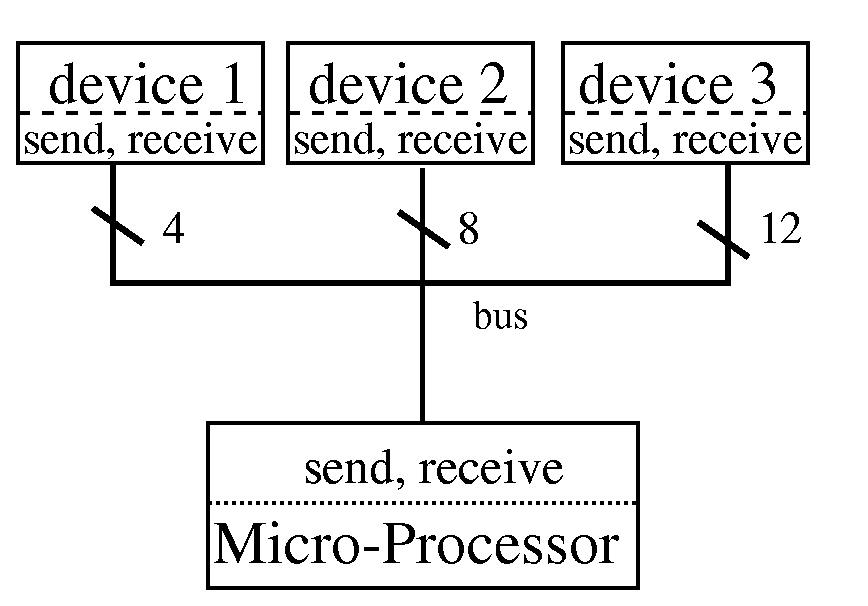Further, we assume a synchronous bus structure where ordering of data transfer between different channels is fixed. Figure 1 depicts a sample bus structure. Given , the switching frequency of the bus, and , the capacitance of the bus, power is computed using the following formula [9]:

Power = C ·  V2 · f

In our calculations we exclude V2, bus voltage, assuming that it is invariant.

Figure 1. Sample bus structure

Given the above model, we would like to devise an algorithm to explore total bus power for any possible bus width and encoding scheme. We consider the following encoding schemes:

Bus-invert was discussed in the previous work section. We define equal-split and don't-care-padding next.

In sending an item whose size is greater than the bus width, time- multiplexed communication is used, i.e., the data item is split and sent into pieces. One way to do this splitting is to send as much of the data as possible each time using all available bus lines, plus a possible last transmission of the remaining bits. Using equal-split an item is broken into equal sized pieces for time-multiplexed transmission. To illustrate how equal-split works, imagine sending an 8-bit data item over a 5-bit bus without equal-splitting the data. Here, two transfers are required to send all 8 bits. The first transfer will send 5 out of 8 bits and the second transfer will carry the remaining 3 bits with 2 bits forced to 0, for a total of 10 transmitted bits, an average of 5 transitions/item. The equal-split technique breaks the 8 bit data into two equal sizes for time-multiplexed transmission, 4 in this case, for a total of 8 transmitted bits, an average of 4 transitions/item.

In sending an item or a piece of an item (note: the paper currently says item, but this applies to pieces also) whose size is less than the bus width, we must decide on how to set the remaining unused bus lines. One way to do it is to set these to logic 0. Using Don't-care-padding, these extra bus lines are unchanged by the sending device and ignored by the receiving device. To illustrate how don't-care-padding works, consider sending an 8-bit data item followed by a 4-bit data item over an 8-bit bus. Without don't-care-padding, after sending the first item, the 4 most significant lines of the bus are forced to 0 and the second item is transmitted resulting in an average of 4 transitions/item. With don't-care-padding the 4 most significant lines of the bus are unchanged when the second item is transmitted resulting in 2 transitions/item.

4. Exploration Algorithm

Given a set of communication channels 1, 2... p , the corresponding data sizes n1, n2, ..., np, and the transfer rates, m1, m2, ..., mp, the following general algorithm explores all possible bus configurations and selects the optimal bus in terms of power. Specifically, the algorithm takes as input a set of communication channels and returns a bus width, and a combination of bus-invert, equal-split, and don't-care- padding that is optimal for low power. 

Input : { C1, C2, C3 ... CP};
Output: bus_width, bus_invert, 
        equal_split, no_care_padding;

ComputeOptimalBus{


CommunicationChannelSet ccs = { C1, C2, ..., CP};

for(m_power=INF, width=1; width < MAXW; width++) {
     for bus_invert 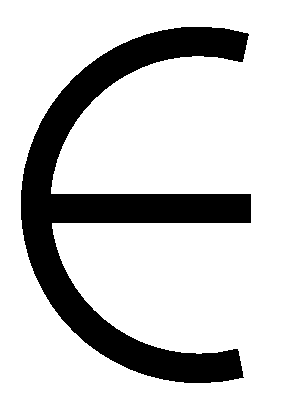 {true, false}
          for equal_split  {true, false}
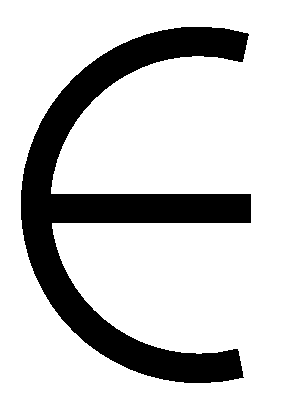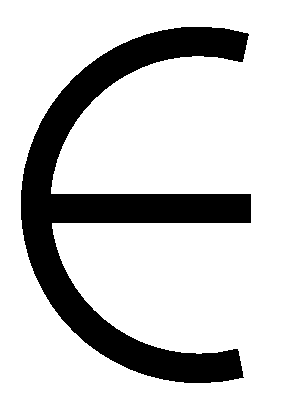               for no_care_padding  {true, false}

                    power = Buspower(ccs, width, 
                                     bus_invert,
                                     equal_split, 
                                     no_care padding) +
                          Extrapower(ccs, width, 
                                     bus_invert,
                                     equal_split, 
                                     no_care_padding);

                    if( power < m_power) {

                       m_power = power;
                       m_width = width;
                       m_bus_invert = bus_invert;
                       m_equal_split = equal_split;
                       m_no_care_padding = no_care_padding;
                    }


     }
     return<m_width, m_bus_invert, 
             m_equal_split, m_no_care_padding›;
}

In the above algorithm, for every possible bus configuration, two functions, BusPower, cost function calculating power consumed by the bus, and ExtraPower, cost function calculating power consumed by the extra circuit required to implement the given encoding scheme, are called to get the total power. The bus width and encoding scheme with the minimum power consumption is outputted as the optimal bus configuration. The complexity of the above algorithm is:

O(k · 2c)· (T(BusPower) + T(ExtraPower))

where k is the maximum bus width, and c is the number of encoding techniques. In this algorithm, c is 3 (bus-invert, equal-split, and don't-care-padding), and T(BusPower) and T(ExtraPower) are time complexities of the corresponding cost functions. These cost functions are based on reading a trace file or are estimated via a formula. In the former case, the time complexity of these cost functions is on the order of the size of the trace file. In the latter case the cost function has a constant time complexity. We discuss these cost functions next.

5. Calculating Bus Power

5.1 Homogeneous Channel-Random

Consider a set of communication channels with equal data-size, i.e., one or more devices transferring data of size n bit, across a bus of size k bit, with a combined transfer rate of m items/second. Assuming that the sent and received data is random in nature [10], we can estimate power, or more precisely bus transitions/second for different bus widths with different bus configurations. First we calculate power for a standard bus with bus-size equal to data size, i.e., k = n:

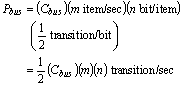
By extending this formula for a bus with narrower size, i.e., k <= n, we get:

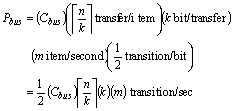
In the above formula, more power is consumed when k does not divide n equally, i.e.:

Thus, for a homogenous set of communication channels, the bus width should be selected such that the data size is a multiple of the bus size. In the case of equal-split, the following formula is used to estimate bus power.

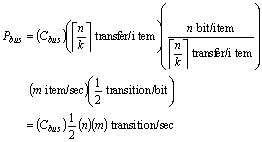
Note that the bus number of transitions is independent of the bus width when equal-split is used. In reality, sending data over a smaller bus is slower and requires extra circuit. However, a narrower bus may have less capacitance compared to a wider bus. Thus it is not clear what bus width will result in minimum power unless all these factors are considered. We examine these other factors later in this paper.

We now extend our formulas for a bus implemented using bus-invert. Here we assume that the bus is k+1 lines wide. (One extra line for the bus-invert control signal.) Let us first assume that the bus size is equal to data size, i.e., k = n:

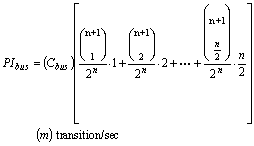
The term in the big bracket computes the average transitions per item. The terms in the summation are the probability of 1, 2, ...., n/2 transitions times the corresponding power. We now extend this formula for a bus with narrower size, i.e., k <= n:

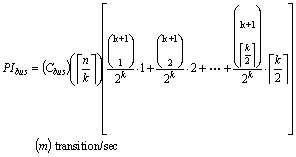
Again, evaluating this formula for k values that divided n equally will result in lower power than k values that don't divide n equally. Using similar arguments that we made earlier, equal-split will reduce the above formula to:

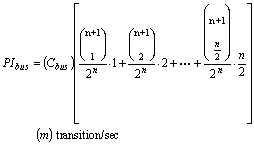
Here too, bus number of transitions is independent from the bus width. But, extra circuit power and different capacitance for different bus widths must be considered for accurate power estimation. We examine these later in this paper.

Using the formulas presented in this section, bus power for a homogenous set of channels with random data can be estimated in constant time. In the next section we give cost functions for a heterogeneous set of communication channels.

5.2 Heterogeneous Channels-Random

Let us now consider a set of heterogeneous communication channels, i.e., a number of devices with different data sizes, communicating over a single bus with size k bit, in a pre-determined order. For each channel 1, 2,..., p , we are given the corresponding data sizes n1, n2, ... , n p as well as the transfer rates, m1, m2, ... , mp . We assume that when bus width k is larger than data size n, only n out of the k lines of the bus are used and the rest are ignored, i.e., we use don't-care-padding. To estimate power for a heterogeneous set of channels, assuming random data as before, we use our standard power formula (no bus invert) used for homogeneous set of channels as follows:

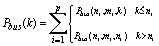
When bus-invert is used, all channels that have data size n <= k, will take less and less advantage of bus-invert, because bus invert saves bus transitions only when more than k/2 bits change value. When n <= k/2, bus-invert will have no advantage at all. To compensate for this, we use the following formula:

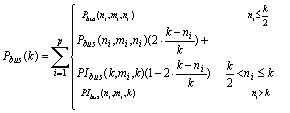
Looking closely at the formula, for n <= k/2, bus-invert will not be utilized at all; therefore we use the non bus-invert power function. For, n > k, bus-invert will be fully utilized, thus we use the bus-invert power function. For all n in between these two extremes we take a weighted-average of the two bus power functions. When n = k, the standard bus power function is weighted with 0 and the bus-invert power function is weighted with 1. Conversely, when n = ½, the standard bus power is weighted with 1 and the bus-invert power function is weighted with 0.

We have given formulas to estimate power consumed by a bus. These formulas can be implemented in software with a constant running time. In the next section we look at using a trace file to manually count the number of bus transitions.

5.3 Trace File - Non-Random

So far, all our formulas have been based on the assumption that the items communicated over the bus are random in nature. This, although a good approximation in general, may not be the case. For example, consider a single channel where device A is sending 8 bit ASCII text characters to device B over an 8-bit bus at a rate of 10,000 items/second. Assuming no bus-invert, our power function will compute power to be:

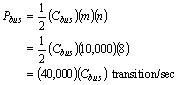
In reality, we know that most text characters use the lower 7 bits for text encoding, thus the probability of the most significant bit changing in value from item to item is closer to 0. With this knowledge, we can compute a better power estimate:

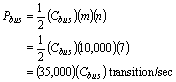
Here, our power formula over estimated the power by 14%, a significant quantity. In this case, if the bus width is changed to 4, the above correlation is destroyed when the text characters are broken into half for time-multiplexed communication. In actuality, much correlation like that may exist among the data and will be neglected when the random estimation model is used.

When a trace file, a listing of all items send/received over a bus, is available, one can write a program to simulate a bus of size k and calculate the actual number of transitions. This brute-force method will be costly but can serve as a very accurate estimation technique. Trace files can be obtained by simulating the VHDL description of a system and recording data transmission among the VHDL processes that use a given bus (signals vectors.)

Calculating bus transitions using a trace file will be more accurate than using an estimation formula, but will require linear time, O(size of the file). This may not be feasible, when the exploration space is large, because for each bus configuration, the above trace file must be processed.

5.4 Bus-logic Power Estimation

Thus far we have looked at bus power in terms of bus transitions times bus capacitance. We have assumed that the bus is implemented using one or more combinations of bus-invert, equal-split and don't-care-padding techniques. Moreover, when the bus width is less than the data size, time-multiplexed communication circuits is added. The power consumed by these extra circuits must be considered. Based on [9], an upper bound on power for the extra circuit needed to implement bus-invert is given by:

In the case of equal-split and don't-care-padding, an upper bound on power is given by:

An upper-bound is sufficient in most cases, because Cextra<<Cbus. Moreover, an exact calculation will depend on the implementation used. Next, we need to consider the difference in capacitance for various bus-widths.

5.5 Bus Power and Capacitance

We will further revise our bus power functions to consider bus capacitance as a function of the internal capacitance and bus width.

Here, is the ratio between internal and external capacitance and is the additional amount of capacitance for a new added bus line. Our capacitance formula is inexact, but it serves as a good first attempt to model all aspects of bus design for reduced power. Let us now define total power to be:

Putting it all together, by combining the above power formulas for bus and extra circuits, one can explore different bus widths for a given communication channels by selecting appropriate and values. We demonstrate this in the next section.

6. Results - GPS Navigation System

We have applied the exploration algorithm given in this paper to a set of homogeneous communication channels with 8-bit data sizes. Our data was randomly generated and consisted of 20,000 samples corresponding to 1-second simulation time. We first calculated the estimated power consumed by the bus for a given bus configuration. Later, we estimated power consumed by the extra circuit required to implement the given bus configuration. The sum of these two estimates gives the total power consumption. A bus configuration consists of a permutation of the 3 optimization methods studied in this paper (equal-split, don't-care-padding, bus-invert.) Tables 1 and 2 give the total bus power, as percent improvement over a standard 8-bit bus using and respectively. Negative values correpond to an increase in power consumption while positive values correspond to a decrease in power consumption when compared to a standard 8-bit bus with no optimization. In these tables, the rows correspond to different bus widths while the columns correspond to the different bus configuarations.

Size Std Eq NoC Eq,
NoC		 Inv Inv,
Eq		 Inv,
NoC		 Inv,
Eq, NoC
1 0 0 0 0 0 0 0 0
2 2 2 2 2 26 27 26 28
3 -9 1 1 1 18 26 28 26
4 2 2 2 1 26 26 27 25
5 -23 0 0 0 8 25 28 24
6 -49 0 0 -1 -12 24 25 24
7 -75 -2 -2 -2 -32 24 24 22
8 0 0 0 0 24 24 26 27
Table 1. Simulated System - Total power-usage improvement (%) with
Size Std Eq NoC Eq,
NoC		 Inv Inv,
Eq		 Inv,
NoC		 Inv,
Eq, NoC
1 -21 -23 -23 -25 -21 -23 -23 -25
2 -8 -9 -9 -11 15 15 13 14
3 -18 -8 -8 -10 7 13 16 11
4 -2 -4 -4 -6 19 18 19 15
5 -29 -7 -7 -10 0 15 17 11
6 -56 -10 -10 -13 -22 12 13 10
7 -84 -14 -14 -17 -44 9 9 4
8 0 0 0 -2 22 20 22 21
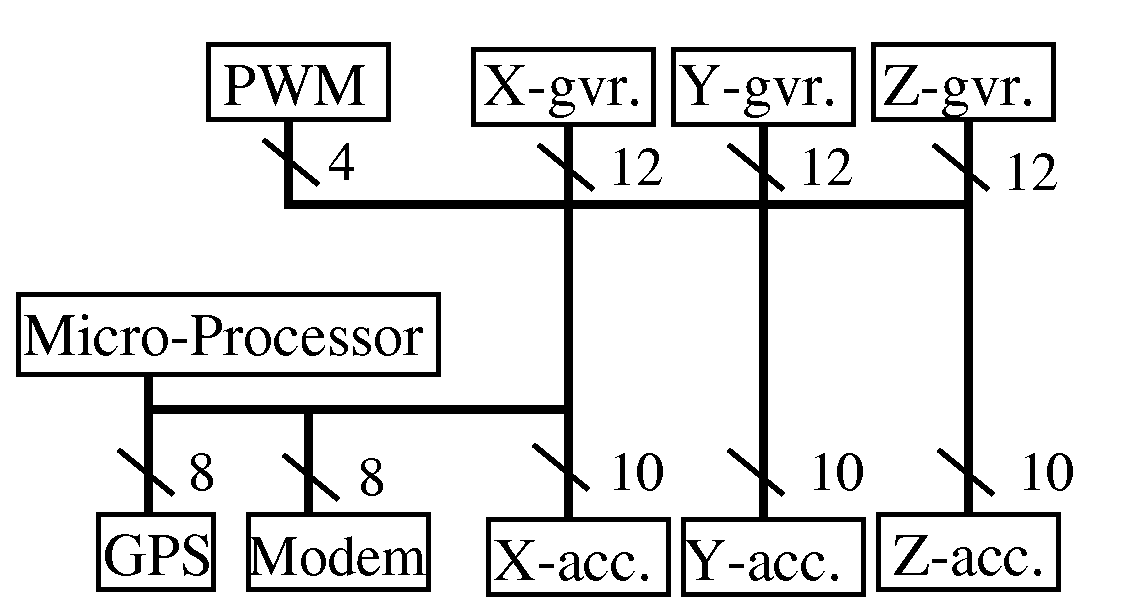
Table 2. Simulated System - Total power-usage improvement (%) with

Using the approach given in this paper, we explored some possible bus configuration for an automobile navigation system composed of 4 communication channels connecting 9 devices to a microprocessor using a single bus. Figure 2 depicts the navigation system's bus structure. In short, our test case involves the following parameters:

n1   =   4,   n2   =   8, n3   =   10,   n4   =   12
m1   =   70,   m2   =   864, m3   =   300,  m4   =   60

Tables 3 and 4 give imorvement of bus power over the original standard 8-bit bus for two different and values. Here, negative values imply an increase in power consumption while positive values imply a decrease in power consumption.

Figure 2. Bus structure for GPS Navigation System

Size Std Eq NoC Eq,
NoC		 Inv Inv,
Eq		 Inv,
NoC		 Inv,
Eq, NoC
1 20 20 20 20 20 20 20 20
2 21 20 20 20 43 43 45 43
3 8 20 20 20 33 47 45 46
4 15 19 19 19 39 44 47 46
5 15 19 19 19 39 44 47 46
6 -12 18 18 17 17 42 41 44
7 -32 17 17 16 26 42 43 40
8 0 17 17 16 26 42 43 40
9 -13 16 16 15 1 40 43 43
10 -4 15 15 15 23 42 42 45
11 -15 14 14 14 -9 39 42 42
12 -21 14 14 13 10 39 40 40
Table 3. Navigation System - Total power-usage improvement (%) over a standard 8-bit bus with a =1000, =10.
Size Std Eq NoC Eq,
NoC		 Inv Inv,
Eq		 Inv,
NoC		 Inv,
Eq, NoC
1 4 3 3 2 4 3 3 2
2 11 10 10 9 35 34 36 33
3 0 11 11 10 25 38 37 36
4 9 13 13 12 33 38 40 39
5 0 13 13 12 17 37 42 36
6 -17 12 12 11 11 36 35 37
7 -37 11 11 10 -10 36 40 34
8 -1 15 15 14 23 38 40 36
9 -13 14 14 13 0 37 40 39
10 -2 16 16 15 23 41 40 42
11 -12 16 16 14 -8 38 41 39
12 -17 16 16 15 11 38 40 39
Table 4. Navigation System - Total power-usage improvement (%) over a standard 8-bit bus with =200, =1/10.

Exploring possible bus configuration and selecting the optimal bus, in the case of the GPS navigation example as well as the random data set, resulted in an estimated power improvement of 22 to 47%. Moreover, the optimal bus was not seemingly an obvious choice.

7. Future Work

Future work can integrate the above bus power estimation algorithms with algorithms for calculating latency and throughput as well as extra circuit area for buses with various width and configurations. This is essential for meeting speed and area constraints while reducing bus power dissipation.

For a given set of communication channels, one can examine multiple bus partitions as well as segmented bus structures to find an optimal solution for reduced power. Such exploration will likely result in an exponential number of possible bus configurations. The partitioning problem is NP-complete, thus, heuristics must be formulated to solve the problem in a reasonable amount of time. Likewise, reordering of the sent and received data can also lead to reduced switching and power consumption, but like partitioning, this approach will require advanced heuristics.

It is desirable to have tools that can generate the extra circuits that are required to implement a given bus configuration. These tools should be capable of automatically generating circuits for bus-invert, equal-split, time-multiplexing and any other coding scheme. Ideally, core integration will use an abstract send and receive protocol and allow these tools to implement the low-level details of communication.

Finally, research should focus on gaining a better understanding of the relative ratios of internal vs. external capacitance. However, these ratios are likely to be very implementation specific. We continue to combine bus parameterization, power estimation and capacitance modeling with the idea of reference-design in an ongoing project called Dalton.

8. Conclusion

We have demonstrated the large power-optimization potential now possible due to the use of on-chip cores, whose interfaces are flexible. Variations in capacitance among different technologies cause the optimal bus to differ even for the same application. We also showed that effects of bus configuration parameters, such as bus width, bus-invert, equal-splitting and don't-care padding, also varies greatly. Therefore, future investigation of new bus configuration parameters and of bus synthesis heuristics can yield significant optimization potential.

9. Acknowledgement

A Design Automation Conference Graduate Scholarship and a NSF grant No CCR9811164 supported this research. We are grateful for this support.

References

[1] Mircea R. Stan, Wayne P. Burleson, "Limited-weight codes for low-power I/O, " Int. Workshop on Low Power Design, April 1994.

[2] Mircea R. Stan, Wayne P. Burleson, "Coding a Terminated Bus for Low Power, " Great Lakes Symp. on VLSI, pp. 70-73, March 1995.

[3] P. Vuillod, L. Benini, G. Micheli, Re-mapping for low power under tight timing constraints, " Low Power Electronics and Design , 1997.

[4] Pai Chou, Ross B. Ortega, Gaetano Borriello, "Interface Co-Synthesis Techniques for Embedded Systesm, " IEEE/ACM International Conference on Computer-Aided Design, pp. 280-287, November 1995.

[5] Michael Gasteier, Manfred Glenser, "Bus-Based Communication Synthesis on System-Level, " in Proceedings of the ISSS, pp. 65-70, November 1996.

[6] Sanjiv Narayan and Daniel D. Gajski, "Synthesis of System-Level Bus Interfaces, " in Proceedings of the EDAC, 1994.

[7] W. Tan, T. Meng, "Low-power Polygon Renderer for Computer Graphics," Int. Conf. on A.S.A.P. , pp. 200-213, 1993.

[8] Enrico Macii, Massoud Pedram, Fabio Somenzi, "High-Level Power Modeling, Estimation and Optimization, " in Proceedings of DAC, pp. 504-511, 1997.

[9] Mircea R. Stan, Wayne P. Burleson, "Bus-Invert Coding for Low Power I/O, " IEEE Transactions on VLSI, March 1995.

[10] A. Shen, A. Ghosh, S. Devadas, K. Keutzer, "On Average Power Dissipation and Random Pattern Testability," ICCAD-92, pp. 402-407, Nov. 1992

[11] D. Dobberpuhl et al. "A 200-MHz 64-bit Dual-Issue CMOS Microprocessor," IEEE Journal of Solid-State Circuits, pp. 1555-1567, Nov. 1992.

[12] C. A. Neugebauer, R. O. Carlson, "Comparison of Wafer Scale Integration with VLSI Packaging Approaches, " IEEE Transactions on Components, Hybrids, and Manufacturing Technology, pp. 184-189, June 1987.

[13] R. Wilson, "Low power and Paradox," Electronic Engineering Times, pp. 38, Nov. 1, 1993.

[14] E. Hwang, F. Vahid, Y. Hsu, "Functional Partitioning for Reduced Power, " Submitted to ICCAD, 1998.

Back to Dalton Homepage