Theorem: Any regular language can be described by a regular expression. In other words, if L = L(A) for some DFA A then there exists a regular expression R such that L(R) = L.
To prove the theorem, given A, we will construct R equivalent to A. The proof is by state elimination. We start with our original automaton (actually, it will be slightly modified), and gradually remove states. The intermediate steps will not really be FAs nor regular expressions. They will be hybrid creatures that have states and transitions, but the transitions will be labelled with regular expressions. For example, we may have a transition from p to q on an expression, say, E = 00(0+11)*0. The meaning of this is that while in p we can move to q on any string that belongs to L(E). For the above example, we can move from p to q on 00110 but not on 010. Note that it means that we can "read" several symbols from input on one transition.
We now describe the construction. First, we will convert A to an equivalent automaton that has no transitions into the initial state, and no transitions out of the final states. We will also convert multiple transitions into a single transition. Then we will execute state elimination. When we're done, we will be left with two states, one initial and the other final, with just one transition between them. The expression labeling this transition is our desired expression R.
Initialization. We modify A as follows.
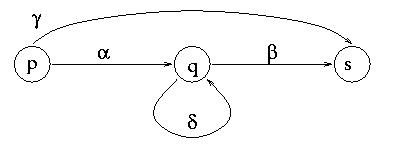
State Elimination. We now iterate the following process until there are only two states left. Pick any state q other than q'0 and qf. We will eliminate q. In order to do so, we proceed as follows: For any pair of states p and s (other than q), denote by a the expression on transition p-> q, by b the expression on transition q-> s, by g the expression on transition p-> s, and by d the expression on transition q-> q (self-loop), as in the picture below:

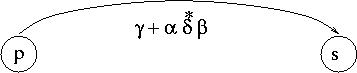
After we do the above for all pairs p and s, we remove q. (We actually only need to worry about pairs p and s that have transitions p-> q and q-> s.)
Note that it is possible that p = s
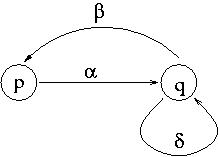
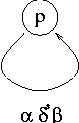
When we are done, we will be left with only two states, q'0 and qf. The expression on the transition from q'0 to qf is the expression R that we are seeking. At all steps, the intermediate automata were equivalent to the one we started with. So also R is equivalent to A.
Note that in the above construction we never used the fact that A is deterministic. So the construction works for NFAs as well.
Example. Let us apply the construction to the following NFA:
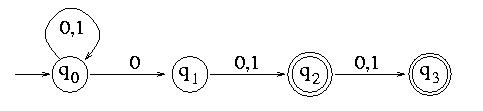
Note that this automaton accepts the set of strings whose 2nd or 3rd last letter is 0. After initialization, we get:
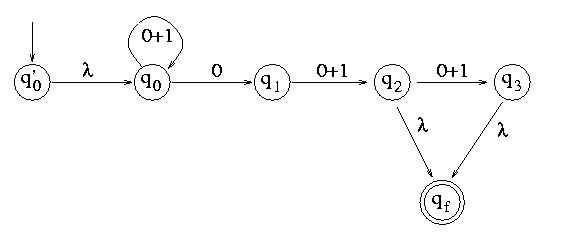
After eliminating q3, we get:

After eliminating q1 and q2, we get:
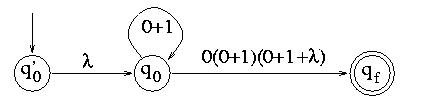
And finally, after eliminating q0, we get:
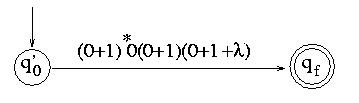
So the resulting expression is (0+1)*0(0+1)(0+1+ l), and we are done.