neal young / Young15Nearly
-
working paper(2016)
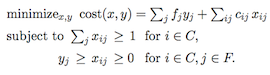We describe the first nearly linear-time approximation algorithms
for explicitly given mixed packing/covering linear programs, and for
(non-metric) fractional facility location. We also describe the
first parallel algorithms requiring only near-linear total work and
finishing in polylog time. The algorithms compute
\((1+\epsilon)\)-approximate solutions in time (and work) \(\tilde
O(N/\epsilon^2)\), where \(N\) is the number of non-zeros in the
constraint matrix. For facility location, \(N\) is the number of
eligible client/facility pairs.
© Copyrights are reserved by the publishers.
Download for personal and limited academic use only.