neal young / Kolliopoulos05Approximation
-
Journal of Computer and System Sciences 71(4):495-505(2005); FOCS'01
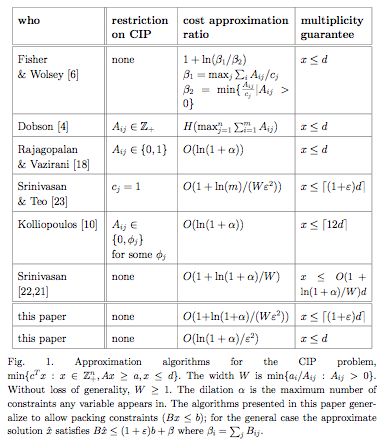Given matrices A and B and vectors a, b, c and d, all with
non-negative entries, we consider the problem of minimizing c\(\cdot\)x
subject to x\(\in Z^n_+\), Ax ≥ a, Bx ≤ b, and x ≤ d.
We give a bicriteria-approximation algorithm that, given
\epsilon\(\in\)(0, 1], finds a solution of cost O(log(m)/\epsilon2)
times optimal, meeting the covering constraints Ax≥a and
multiplicity constraints (x≤d), and satisfying Bx≤(1 + \epsilon)b + β,
where β is the vector of row sums, β_i=\(\sum_j\) Bij.
Here m is the number of rows of A.
This gives an O(log m)-approximation algorithm for CIP --- minimum-cost covering integer programs with multiplicity constraints, i.e., the special case when there are no packing constraints Bx ≤ b. The previous best approximation ratio has been O(log maxj \(\sum_i\)Aij since 1982. CIP contains the set cover problem as a special case, so O(log m)-approximation is the best possible unless P=NP.Journal version of Tight approximation results for general covering integer programs.
© Copyrights are reserved by the publishers.
Download for personal and limited academic use only.