• SIAM Journal on Computing 41(3):684-713(2012); STOC'02

  With Mordecai Golin and Claire Mathieu
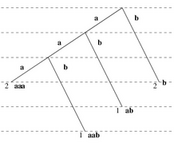  We study the generalization of Huffman Coding in which codeword letters have non-uniform costs (as in Morse code, where the dash is twice as long as the dot). Despite previous work by many authors including Richard Karp [1961] and Kurt Mehlhorn [1980], the problem is not known to be NP-hard, nor was it previously known to have a constant-factor approximation algorithm. The paper describes a polynomial-time approximation scheme (PTAS) for the problem. The algorithm computes a \((1+\epsilon)\)-approximate solution in time \(O(n + f(\epsilon) \log^3 n)\), where \(n\) is the input size.

  Journal version of [2002].

  • more...
  •   full text
    
  •   slides
    
  •   bibtex
    
  •   google scholar
    
  •   doi
    

© Copyrights are reserved by the publishers.
Download for personal and limited academic use only.