The Steiner tree problem

Problem definition: Given a weighted  undirected graph G(V,E), and a set S subset of V find the Minimum-Cost tree that spans the nodes in S. This problem is known in the literature as the Steiner tree problem.  Let M the number of nodes in S, which we will call participants.

The problem is NP-complete, which means that there is no known *polynomial* algorithm that will find the exact solution of the problem. However, there are algorithms that solve the Steiner problem in exponential time (O(2^N)  or O(2^M)).
 

Exact solution algorithms

Topology Enumeration algorithm (Hakimi). We find all possible trees that span the  the S nodes. The algorithm finds all the minimum spanning trees (MST) for the subset W where W includes S: W = S u {some more nodes of V}.   As you can see, for W we have many possible choices  O(2^(N-M)) and we have to try all of them!

Dynamic programming.  Decompose graph in two parts, solve the problem for each part and then combine the solutions.
 

Approximate solutions

Undirected graph. CR is the competitive ratio of the algorithm, i.e., how good the approximation is in the worst case.  It is defined as the maximum Talg / Topt,
where Talg is the cost tree of the algorithm, and Topt is the cost of the optimal solution.

The Naive or Shortest Paths algorithm.
Find the Shortest path tree from one participant node to the rest of the graph.
Prune the parts of the tree that do not lead to a participant.
Complexity O(N^2),  CR = O(M).

The Greedy or Nearest Participant First  algorithm.
Start from a participant.
Find the participant that is closest to the current tree.
Join the closest participant to the closest part of the tree.
Repeat until you have connected all nodes.
Complexity O(M N^2),  CR = O(1), actually CR  <= 2.

The Rayward-Smith algorithm. (Not presented in class)

The Kou Markowsky and Berman algorithm (KMB).
 1. Find the complete distance graph G'
      (G' has V' = S , and  for each (u,v) in VxV there is an edge with
weight equal to the weight of the min-cost path p_(u,v)  in G)
  2. Find a minimum spanning tree  T' in G'
  3. Translate T' to the G graph, by substituting every edge of T'
with the corresponding path of G. Let us call T the result of the translation.
  4. Remove any possible cycles from T.
Complexity O(M N^2), CR = O(1), actually CR <= 2.
 
 

The proof for the Naive algorithm.

 Lemma 1.
For any graph G(V,E) and any set of paricipants S, M=|S|,
the competitive ratio CR of the Naive algorithm for the Steiner tree problem
is bounded by M-1:

                        CR_naive <= M-1

Proof: Let d_max be the maximum distance between any two participants.
The optimal tree Topt will be at least as large i.e.
                                Topt => d_max                                (1)
 The Naive tree Tnaive will never be more expensive than:
                                Tnaive <= (M-1) d_max              (2)
  This is easy to prove. Select a root among the participants and find all
the shortest paths p_i between the root and every other of the i= 1,...M-1 participants.
 The cost of  of the path of each path p_i is less than d_max, and the total cost of
the Tnaive is the union of these paths, which proves (2).

Now, we  write (1)  as:
                        1/ Topt <=  1/d-max                                  (3)
If we multiply (2)  and (3), we get:
                            Tnaive / Topt <= M-1                         Q.E.D.

Lemma 2.
 There exists a graph G(V,E) and a set of participants S, M=|S|,
such that the ratio of the Naive for the Steiner problem is:

                            Tnaive /Topt = M-1

Proof. I only need to show one instance of the Steiner problem that this
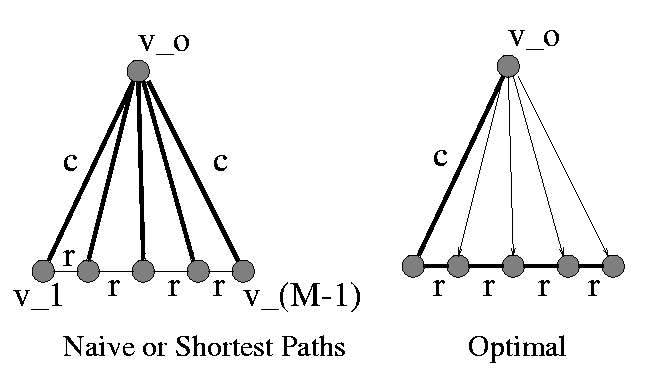
happens.  Assume a graph that has a node v_o that connects to every other
node in the graph v_1 to  v_(M-1), and the cost of the edge:
        w(v_o, v_i) = c
Assume that every node v_1, v_2, .......v_(M-1)  connects
with the previous and the next in this order and v_1 connects with v_(M-1).
The cost of these edges is r, and is infinisimal (really small or r -> 0).
  Assume that all nodes are participants.
 A possible execution of Naive is to pick v_o as root and connect every other
node with the direct edge of cost c.
           Tnaive =  (M-1) * c                                             (1)
  The optimal tree connects v_o  and v_1 and then everybody else with
edges of cost r.
             Topt =  c  +  (M-2) * r       =>
              Topt = c,      for r -> 0                                 (2)
Using (1) and (2):
             Tnaive /Topt = M-1