Instructor: Michalis Faloutsos.
Nine questions in total [120] and [10]: bonus. No programming part this
time.
In this Assignment, you are expected to provide well written and complete
answers. One-word answers, or vague generic arguments will
not get much
this time. Start early and spend time on providing rigorous proofs.
No extension will be granted, so start working early.
1. [10] Exercise 25. 2-4 from the book. p.,531.
2. [10] Exercise 25. 3-3 from the book, p. 535.
Explanation: We want the algorithm complexity to
be in O( (m+1) N^2)
where N the number of nodes.
3. [10] Problem 26.1 page 576: Transitive closure of a dynamic
graph.
Do only:
3.1 [5] 26.1.a.
Just provide *some* polynomial algorithm and calculate
its complexity.
3.2 [5] 26.1.b.
Hint:
Give an example where by adding one edge you can achieve a
many entries in your matrix. Try to think of a case where you can have
N/2 nodes becoming able to reach N/2 nodes.
4. [10] Execute the transitive closure algorithm on the graph
of Fig. 26.2.
Show the matrices for all your
steps, until the algorithm terminates
(if the matrix is the same in
two consecutive steps, the algorithm terminates)
5. [10] Steiner problem:
5.a. [5] Does the competitive
ratio of the Naive algorithm change
when we restrict the edge
weights to only two values: 1 or 2?
Argue/prove your answer.
5.b. [5] What is the
competitive ratio of the Naive if restrict the weight
of the edges to 1
or 2 and we restrict the maximum number of edges
between any
nodes of the graph to be less than K?
Prove your answer.
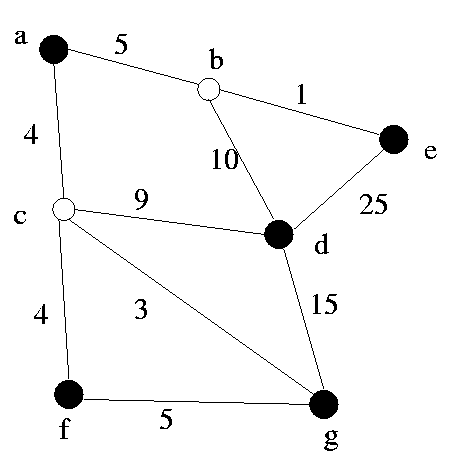
6. [30] Steiner problem. Execute the Naive, the Greedy
and KMB algorithms in the
figure below. Show
the execution of each step and also the approximate Steiner
tree for each algorithm
as it is being created. Don't forget to provide you KMB
Steiner tree at the original
graph G.
Weighted undirected
graph: G = (V, E, weight())
V = {a,b,c,d,e,f,g}
Participants: S = {a, d, e, f, g}
Start building your Steiner tree from node "a" (this
is only for uniformity reasons)

7. [10] Exercise 27.2-2 from the book, p. 599.
You only have to show the series of augmenting paths, ie.do
just the Ford-Fulketson and not the Edwards-Karp. In addition,
take a look at the newly added, explanation of Ford-Fulkeron in my
web-page.
8. [10] Exercise 27.2-3 from the book, p. 599.
9. [10] From the exercise 27-3.5 from the book,
p. 604,
prove *only* that |L|=|R|.
Bonus [10] : Solve exercise 27-3.5
(you do not have to do this, unless
you want the bonus points)