QUESTION 1 :
Algorithm description: There are two functions in this algorithm
(1) int length( node* subroot ): this recursive function accepts a node* subroot as parameter and returns the height of the tree whose root is subroot.
(2) void printout ( node* subroot): this
recursive function accepts a node* subroot as parameter and prints out the
longest path from this node to the leaves.
First of all, this function prints out the value of subroot, because it will be on the longest path for
sure. Then “length” function will be
called on its left and right subtree separately and height of them will be
compared. Then printout function will
be called again by following the longer subtree.
Functions:
(1) void printout ( node* subroot) {
cout << subroot-> value;
if( subroot->left == NULL && subroot->right == NULL) return;
if( subroot->left != NULL ) {
int left_length = length(subroot->left );
}
if( subroot->right != NULL ) {
int right_length = length(subroot->right );
}
mynode = the longer path of right and left branch
printout( mynode );
}
(2) int length( node* subroot ) {
if( subroot->left == NULL && subroot->right == NULL) return 0;
if( subroot->left != NULL ) {
int left_length = length(subroot->left );
}
if( subroot->right != NULL ) {
int right_length = length(subroot->right );
}
int longer_path = right_length >= left_length ? right_length : left_length;
return longer_path + 1;
}
Analyze:
Time complexity: The worst case is that all nodes have only one child. Let n be the number of nodes in the tree and f(n) be the time complexity for function printout and g(n) be the time complexity for function length.
F(1) = 1
F(n) = f(n-1) + g(n-1) = f(n-1) + n-1
By using iteration method, we can derive that f(n) = O(n^2)
Space complexity: The worst case is the same. We need to maintain a stack for all non-returned functions. Each of them needs constant space. For the worst case, functions will starts to return until the last node is called. We need O(n) space.
QUESTION
2 :
(a) first we need to prove: f(n)=O(g(n)) ===> g(n) = W(f(n))
Steps: f(n) = O(g(n)) ===>
there exists a constant c1 and n0, 0<=f(n) <= c1* g(n), for n >= n0 ===>
0 <= 1/c1 * f(n)
<= g(n) for n >= n0. Let c2 = 1/c1.
We can make the proof.
Then we need to prove g(n) = W(f(n)) ===> f(n)=O(g(n)). The step is similar.
(b) To prove this formula, we need to find out a constant c and n0.
10000 n^4 + n^3 log n log n <= 10000n^4 + n^4 = 10001 * n^4
We can choose c as 10001 and n0 as 1;
(3) To prove 0.001 n^2 log n <= c * (100 n^2) for all n >= n0, we need to find out
c and n0. For any c, we can find n0 to make this equation not true.
QUESTION
3:
The statement is true.
The idea of the algorithm is as
follows: for a given path, we record how many times a node is visited on this
path and the location it is visited. If
a node is visited more than once, assuming the first time it is visited is at
location i and the second time it is visited is at location j, the algorithm
will delete all nodes from i+1 to j from the original path. We do this for all repeat nodes. The new
path will be a simple path.
QUESTION
4:
We can use the iteration method
to get the time complexity. Let n be the length of array A and f(n) be
the time complexity. The time for each line is as follows:
Algy(A, i, j ) {
if i+1 >=
j
then return
A;
k = floor( (i+j)/2
)
--------------------------------
constant c
A1 = Algy(A, i,
k) -------------------------------- f(n/2)
A2 = Algy(A, k+1,
j)
--------------------------------
f(n/2)
A3 = Combine(A1,
A2)
--------------------------------
O(m1 + m2) = O(n)
return A3
}
Analyze: f(1) = 1
f(n) = 2 f(n/2) + O(n)
= ……..
= n logn
(the iteration step is the same as merger sort, you
have to write the details for the assignment and test.)
QUESTION 5:
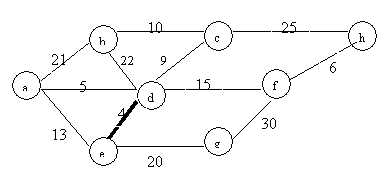
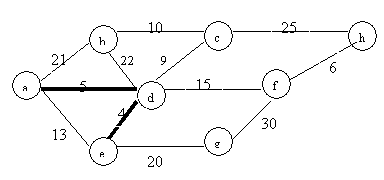
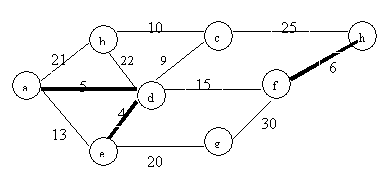
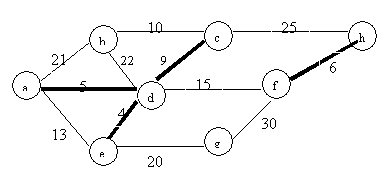
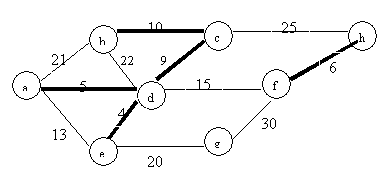
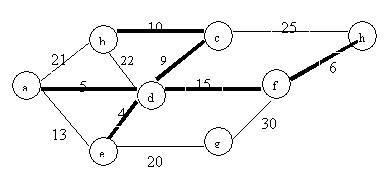
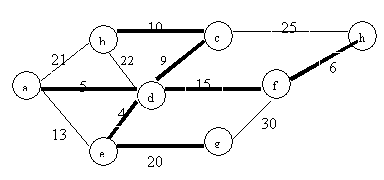
If we run Kruskal’s MST algorithm, we will examine and select edges according to the weight in increasing order. For the rescaled graph, the sequence of the weight will not be changed. Run the same algorithm on the same graph with different scale, the MTS will be the same.
QUESTION 6:
Algorithm description: There are three functions in this algorithm
(1) offCenter(): This function is called from main and return value is the absolute value of the difference of the left and right lengths.
(2) int
get_left_length ( node* this_node ): this
is a recursive function which accept a node* as parameter and return the length
from this node to the very left end.
(3) int
get_right_length ( node* this_node ): this
is a recursive function which accept a node* as parameter and return the length
from this node to the very right end.
Functions:
int final_value = mynode -> offCenter();
(1) int offCenter() {
int left_length = get_left_length ( mynode );
int right_length = get_right_length ( mynode );
return abs(left_length – right_length); }
(2) int get_left_length ( node* this_node ) {
if (this_node -> left == NULL ) return 0;
else {
return get_left_length ( this_node->left ) + 1;
}
}
(3) int get_right_length ( node* this_node ) {
if (this_node -> right == NULL ) return 0;
else {
return get_right_length ( this_node->right ) + 1;
}
}
Analyze:
Time complexity: Let n be the length of list and f(n) be the time complexity. Each node is visited once. The time would be O(n).
QUESTION
7:
(1) BFS
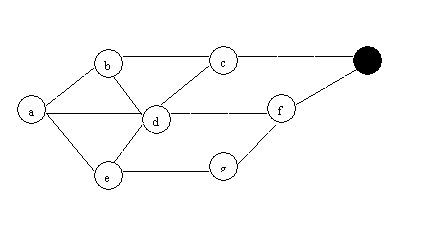
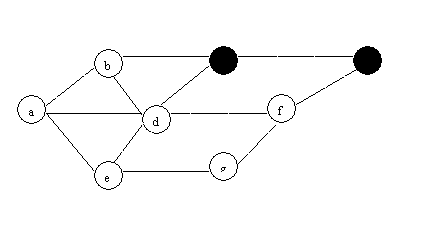
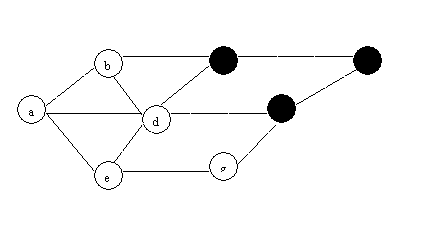
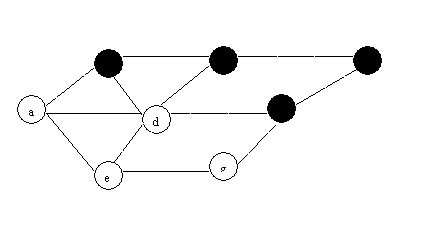
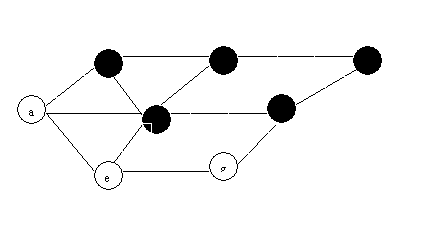
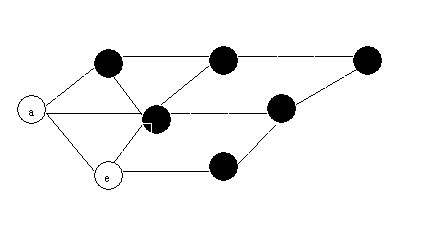
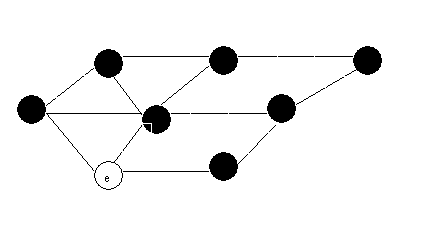
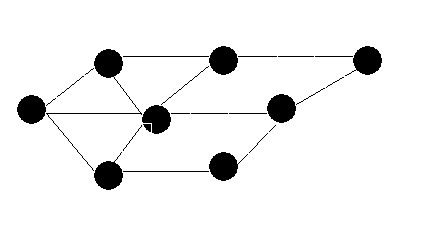
(2)DFS:
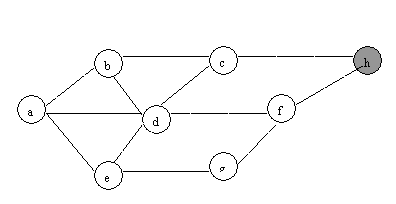
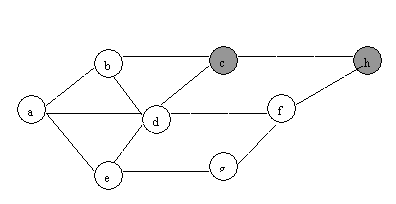
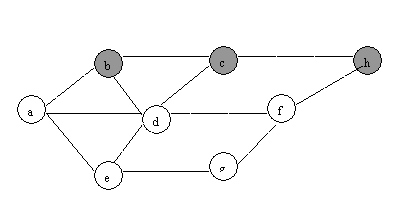
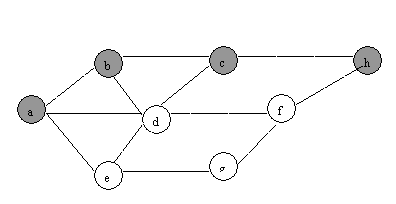
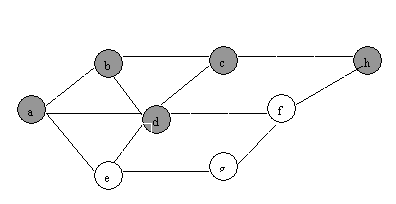
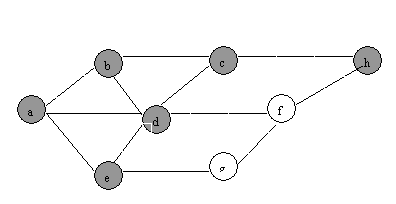
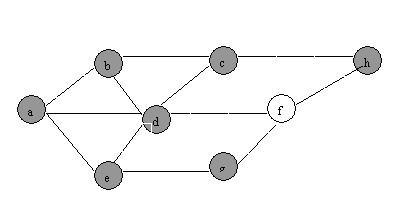
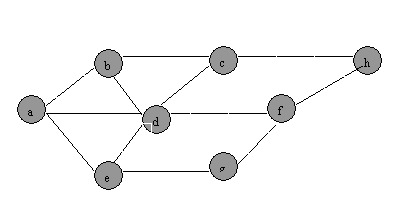
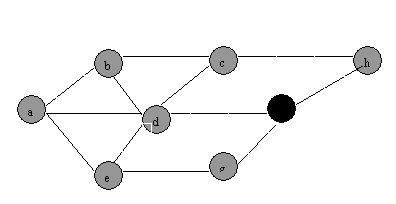
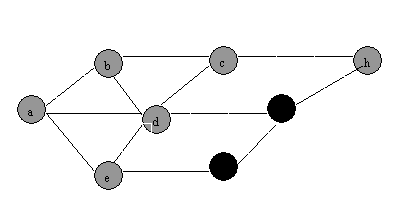
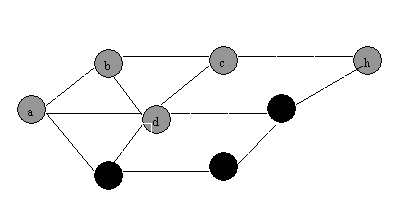
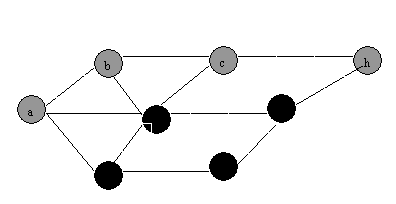
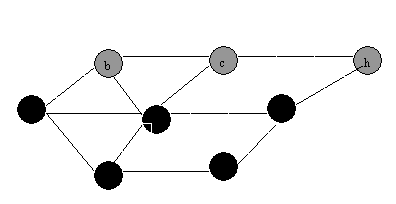
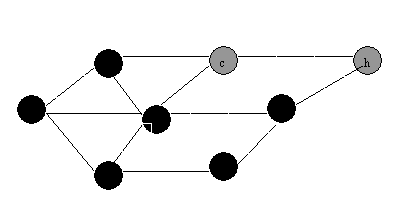
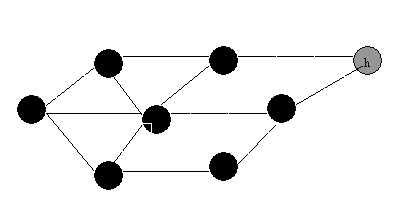
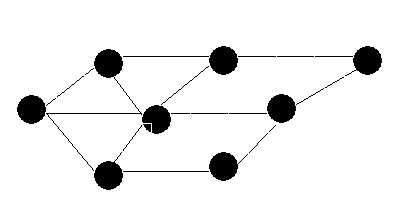
QUESTION
8: the order is: d-e,
d-a, f-h, d-c, b-c, d-f, e-g