Version 1.0 MAKE SURE YOU CHECK FOR UPDATES.
PART A. Written part.
1. [20] Assume a weighted connected undirected graph
$G(V,E, w())$ and assume
that all the weights of the edges are distinct integers (no two weights
are equal).
Prove or disprove the following statement:
For any pair of nodes of the graph,
the minimum cost path between them is unique.
2. [20] Prove the following.
a.[10] What is the minimum
and maximum number of edges you can have in a graph?
Note: The edges should be expressed as a function of N.
b. [10] A connected
graph G(V,E), will have at least |V| - 1 edges.
Use induction and make sure
you write clearly the induction steps.
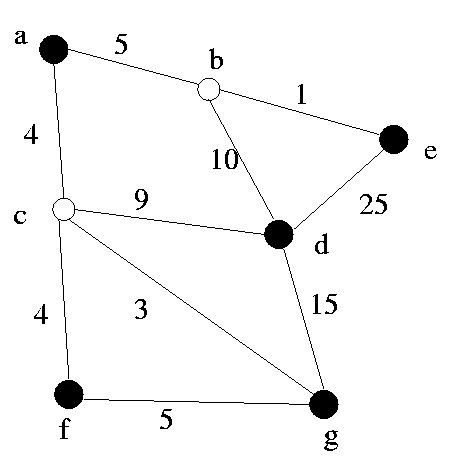
3. [20] In the graph below, you are at node "e" and
you want to create a tree to communicate
with your friends
(the other black nodes: a,d, f, g) . The weights can be interpreted in
two different ways.
1. Weight = Delay.
Calculate the tree that minimizes the end to end delays
from you to all your
friends. I.e. the delay from you to each one of your friends is the
minimum possible.
2. Weight = Cost in
sweet green dollars. Calculate the tree that has minimum total cost.
NOTE: We are
interested in creating a tree to make sure that you and your friends can
communicate.
Explain which algorithm
you will use, and show the creation of the tree one node at a time.
Note that you may
need to modify the tree that you derive from known algorithms.
Show the final tree
that you will use to communicate with your friends.
Show in 1) the
final end-to-end delay from e to every other node, in 2) the total
cost of the tree.
The fees: Every time the boat crosses the river the guard has to pay
taxes to evil Michalorg,
supreme ruler of Faloutsonia. The tarif is as follows:
* empty boat: C_e dollars (they are alien dollars
with an exchange rate of 1:10000 to US$)
* Xeron:
C_x dollars per head
* Ommons C_o dollars per
head
The cost is additive: for a ride with 1 Xeron and two Omons, the cost
is:
C_e + C_x + 2 * C_o
Naturally all costs are non-negative (positive or zero).
Every morning, the guard has to transport X Xerons, and
O Omons,
from the A side of the river to the B side of the river without anybody
getting eaten and
with the minimum cost in taxes.
You are friends with the guard and you want to write a C++ program
to help
him find safe and least costly way of boat rides (sum of
taxes payed should be minimum).
The input of the program is the number of Xerons,
X, the number of Omons, O and the costs
C_e , C_x, C_o. Everybody is on the A side
of the river.
The output should be:
a. [10] if there is a way to transfer everybody
across (Print Yes or No).
b. [10] the minimum number of times that
the boat has to cross the river
(total crossings in
either direction).
c. [30] the exact sequence of states and moves of
a safe for all trip.
The required output
is like this:
A -> B:
X_a O_a
move 1, 1
B -> A:
X_a-1 O_a - 1 move 1, 0
where X_a
O_a is the number of creatures on side A before you put anyone in
the boat,
and "move 1, 1" means that you intend
to move one Xeron and one Omon from the X_a and O_a.
In the second line, "move 1 0"
means that you intend to move 1 Xeron from B to A.
-------------------------------------------------------------------
Bonus 1 (+10%): Provide
a clever way to terminate the search as early as possible.
Find it, describe it, explain
why it is correct and implement it.
Bonus 2 (+10%): Find the
minimum number of rides required to transfer the creatures, independently
of the associated cost.
---------------------------------------------------------------------
ATTENTION: YOUR PROGRAM SHOULD RUN IN LINUX ON hill.cs.
Your executable should be named "run" and it should be run as follows:
$ run filename
Now, filename is the name of a file that contains the problem information
in the following
format:
X
// initial number of Xerons on side A
O
// initial number of Omons on side A
C_e
// tax of empty boat
C_x
// tax for each trasnported Xeron
C_o
// tax for each transported Omon
This file is can be assumed to be correct.
The other 50 points: are the report, the makefile, the programming style, programming efficiency etc.
THE REPORT [50].
a. How you model the problem
b. How your solution works
c. Main data structures, classes and methods
d. Why do you think your solution is correct
(arguments, not proof)
e. What is the complexity of your program.
The report should not be more than three pages (excluding the output
of test cases).
Hints: 1. Think of how you should model the problem. How can
you model a state? Probably a few numbers
are enough From one state, you can go to a number of other
states. A graph may help.
2. It is a good idea to get your computer to explore all possible
moves, and find the best.
3. Make sure your program does not fall into infinite loops. How many times
do you want to consider or visit one state?
4. When do you stop searching for a solution? Do you want to revisit a
state?
WHAT TO SUBMIT
Electronically:
a. your program ready
to compile and your executable named: run
b. your makefile
c. a README file for
instructions on how to run it (they should be as stated but write it nevertheless)
f. the report
e. the output of your
program in the given test cases (to be completed).
A hard copy of your report and your program and output should
be given with the written part of the assignment.
Put names, email, section and lab, as in first assignment.
WARNING: A report that makes false claims about the program will be
considered as cheating.
An output sample that is not generated by the submitted program will also
be considered as cheating.
Check: http://www.cs.ucr.edu/~klick/ the links
for linux (for makefiles) and programming for
stylistic and programming suggestions.