CS-141: Assignment 2

Winter 2002

Prepared by Jin Guo and Michalis Faloutsos

Write your name (LAST, FIRST), 4digits SSN, section and lab. Keep back-up copy electronically or with photocopy.

Answers must be complete. concise and readable: a single numbed or an equation is not an answer.

All answers are worth 10 points.

1: Given a binary tree, design an efficient algorithm to print out the longest path starting from the root node and discuss its time and space complexity (no formal proof needed).

2: Prove that:

a. f(n)=O(g(n)) <=> g(n) = W(f(n))

b. 10000 n^4 + n^3 log n logn = O(n^4)

c. 0.001 n^2 log n =/= O(100 n^2)

3. Consider the following proposition :

“In a graph, if there exists a path between two nodes, then there exists a simple path between them.”

Is the above statement true?

If yes, provide an algorithm to convert any path between two points into a simple path.

If not, give a counter example to disprove the proposition.

4.Consider the following pseudo-code of an algorithm called Algy.

Algy(A, i, j ) {

1. if i+1 >= j

2. then return A;

3. k = floor( (i+j)/2 )

4. A1 = Algy(A, i, k)

1. A2 = Algy(A, k+1, j)

2. A3 = Combine(A1, A2)

3. return A3

4. }

Assume that the calculation of k in line 3 takes constant time and Combine(A1,A2) takes O(m1+m2) time where m1 and m2 are the sizes of arrays A1 and A2. Combine() returns an array of size m1+m2.

Calculate the time complexity of this algorithm.

5 :Assume that the weights in a graph are positive, prove that you can rescale them by adding a constant to all of them or by multiplying them all by a constant without affecting the MSTs, provided that the new weights are positive. Hint: prove that an MST in the first graph is also an MST in the rescaled graph.

6: Given a doubly linked list and one node in this list, design a recursive algorithm and C++ code to calculate how much off center is the node.

Discuss the time complexity.

class lnode {

lnode *left;

lnode *right;

public:

int offCenter();

}

From main, I want to be able to call: p->offCenter(), and have it return 0 if the node is exactly in the middle, or else the absolute value of the difference of the left and right lentgths.

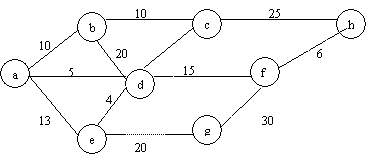
7: Given the graph below, assume node h is the source.

A. Run BFS, show the evolution of the tree one node at a time, write the final value for the depth and parent of each node, write the node sequence according to the first time the node is visited. If a node has more than one neighbors, select alphabetically.

B. Run DFS, and show the evolution of the tree one node at a time. Write the nodes in the order they are visited, and the order they turn black (all children have been visited).

Select nodes in alphabetical order again. Note: assume the recursive procedure we presented in class.

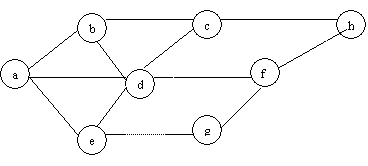
8: Given the graph below, run Kruskal’s MST algorithm. Write the list of edges in the order they are examined and the order with which they are added to the tree.