1.  [10] Exercise 25. 2-4 from the book. p.,531.

2. [10]   Steiner problem:
       a. [5]  Does the competitive ratio of the Naive algorithm change
        when all edges have weight 1?
         Argue/prove your answer.

        b.  [5] What is the competitive ratio of the Naive if all edges
    have weight 1   and  the maximum distance is at most K hops?
          Prove your answer.

3. [10]  Problem 26.1 page 576: Transitive closure of a dynamic graph.
        Do only:
        3.1 [5]  26.1.a.  Just provide *some*  polynomial algorithm and calculate
           its complexity.
        3.2  [5] 26.1.b.
           Hint: Give an example where by adding one edge you can achieve a
            many entries in your matrix. Try to think of a case where you can have
            N/2 nodes  becoming able to reach N/2 nodes.
 

4.  [10] Give an example of a weighted directed graph with negative-weight edges, but no negative-weight cycles, such that
Dijkstra's algorithm runs incorrectly if started from some node of the graph. (see text p. 515)

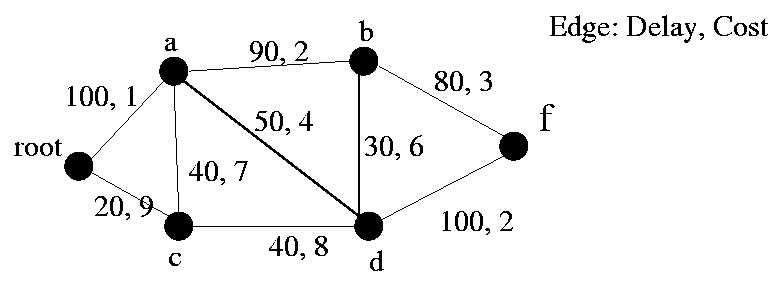
5.  In the network given below, we are at the root and we want to
establish a communication tree with all the other nodes.
Each edge has  a) a delay, and b) a cost value. The delay
shows the delay in milliseconds for transferring data over the edge.
The cost is the amount in sweet US dollars that we have to pay
in order to include (lease) the edge in our communication tree.

     a. [5] Assume that we are only interested in minimizing
the total cost (in $) of the tree that we want to create.
Which algorithm should you use? Which is the tree with the minimum
cost?
    Show the tree, its cost, and the order with which the nodes join the tree
according to your algorithm. Show the tree's evolution one node at a time.

    b. [5] Assume that we are only interested in
minimizing the end-to-end delay (the delay from when you
send the data until a friend receives it) between the root
and each possible destination.
Which algorithm should you use? Which is the tree that minimizes
the end-to-end delays?

Show the tree and the order with which the nodes join the tree
according to your algorithm, and the delay that the delivery
of data towards each destination (the delay of the path on
the tree).Show the tree's evolution one node at a time.

Programming part.  [50]

You are given a directed graph with positive weights. However, the meaning of the weight is available bandwidth.
Given two points in the graph, you want to calculate the path with the maximum bandwith. The maximum bandwidth of a path is the minimum bandwith among each edges.

ATTENTION: YOUR PROGRAM SHOULD RUN IN LINUX ON hill.cs.
   ANYTHING ELSE DOES NOT COUNT.
  Also,  no makefile and no report will severely reduce your grade!!!!!

In more detail, your executable should be named "run" and it should be run as follows:

$ run  < datafile

Your program should handle more than the sample data files given.
The data file should  first give the  total number of nodes, the root of the tree and then pairs of nodes that are connected with an edge:

30                         // total number of nodes
5                            //  start node
3                              //  end nore
1     2         100    // edge (1, 2) with bandwidth 100
2     3          150
. . .
n1     n2     bandwidth

OUTPUT:
[5] The input graph. See samples sample1.txt
[15]  The path with maximum bandwidth:
        " a -> b   with bandwith   b"                     for every edge of the path
[5] The maximum bandwidth

The other 25 points: are the report, the makefile, the programming style, programming efficiency etc.
  More specifically from the 25 points we have:
 A.The report [15 points] is a very important file since you need to describe
     a. how you solve the problem
     b. why do you think your solution is correct (arguements not proof)
 
 B. 5 points are given for coming up with a different algorithm than the basic provided at the end
 even if you implement the basic one. You should argue (not prove) why your algorithm is
 expected to find the correct path.

You need to have classes and methods with the name:
class Graph
Graph::calculateMaxBandPath(......)
Graph::printMaxBandPath(.....)
Graph::readInputGraph(.....)
 

Programs and output

  Electronically: submit
         a. your program ready to compile and your executable named: run
         b. your makefile
         c. a README file for instructions on how to run it
         f. the report in ascii.
         e. the output of your program in the sample datasets  (datasets to be provided)
A copy of your report should be given with the Part I of the assignment.

WARNING: A report that makes false claims about the program will be considered as cheating.
                        An output sample that is not generated by the submitted program will also be cosidered  as cheating.

Check:  http://www.cs.ucr.edu/~klick/    the links for linux (for makefiles) and programming for
stylisitc and programming suggestions.

Hints  and Bonus:  (NEW)

     We provide a basic algorithm that you can use. To get full marks you have
to think of another algorithm and explain why it would work, though you
can implement the basic.  You should also explain why the basic shold work
      For bonus points [10], we should implement your algorithm (INSTEAD of the
basic).

    The basic algorithm for the programming part is the following.
 * Repeat
 *       Find a path from the source to the destination
 *       Remove the bottleneck link of the path from the graph
 * End repeat
 * Among  all the paths you have identified,  keep the one with the maximum bandwidth

Note: bottleneck link of a path is the link with the minimum bandwidth